A water pipe is pointed straight up and water flows out from it with constant volume flow rate, reaching a certain maximum height. In order to make the water reach double the height, which of the following adjustments to the nozzle of the pipe will be required?
(a) Decrease the area by a factor of 2
(b) Decrease the area by a factor of √2
(c) Decrease the area by a factor of 4.
To solve the problem of how to adjust the nozzle of a water pipe to make the water reach double the height, we can follow these steps:
1. Understand the Problem:
We have a water pipe that is pointed straight up, and water flows out with a constant volume flow rate (Q). We need to determine how to adjust the nozzle to make the water reach double the height.
2. Define the Variables:
- Let the initial maximum height reached by the water be h.
- The initial velocity of the water as it exits the nozzle is u1.
- The final velocity at the maximum height is 0 (since the water stops rising at its peak).
- The acceleration due to gravity is g.
3. Apply the Kinematic Equation:
Using the kinematic equation for uniformly accelerated motion:
v2=u2+2as
where v is the final velocity (0 at maximum height), u is the initial velocity (u1), a is the acceleration (−g), and s is the distance (height h).
0=u21−2gh
Rearranging gives:
u21=2gh
Thus, the initial velocity u1 can be expressed as:
u1=√2gh
4. Consider the New Height:
For the new scenario where the height is doubled (2h), we can set up a similar equation:
0=u22−2g(2h)
This gives:
u22=4gh
Therefore, the new initial velocity u2 is:
u2=√4gh=2√gh
5. Relate the Volume Flow Rate:
The volume flow rate Q is constant, given by:
Q=A1u1=A2u2
where A1 and A2 are the cross-sectional areas of the nozzle in the first and second cases, respectively.
6. Substitute and Solve for Area:
Rearranging gives:
A1u1=A2u2
Substituting u1 and u2:
A1√2gh=A2(2√gh)
Dividing both sides by √gh:
A1√2=2A2
Rearranging gives:
A2=A1√2
7. Conclusion:
To make the water reach double the height, the area of the nozzle must be decreased by a factor of √2. Thus, the correct answer is (b) Decrease the area by a factor of √2.
We have a water pipe that is pointed straight up, and water flows out with a constant volume flow rate (Q). We need to determine how to adjust the nozzle to make the water reach double the height.
- Let the initial maximum height reached by the water be h.
- The initial velocity of the water as it exits the nozzle is u1.
- The final velocity at the maximum height is 0 (since the water stops rising at its peak).
- The acceleration due to gravity is g.
Using the kinematic equation for uniformly accelerated motion:
v2=u2+2as
where v is the final velocity (0 at maximum height), u is the initial velocity (u1), a is the acceleration (−g), and s is the distance (height h).
0=u21−2gh
Rearranging gives:
u21=2gh
Thus, the initial velocity u1 can be expressed as:
u1=√2gh
For the new scenario where the height is doubled (2h), we can set up a similar equation:
0=u22−2g(2h)
This gives:
u22=4gh
Therefore, the new initial velocity u2 is:
u2=√4gh=2√gh
The volume flow rate Q is constant, given by:
Q=A1u1=A2u2
where A1 and A2 are the cross-sectional areas of the nozzle in the first and second cases, respectively.
Rearranging gives:
A1u1=A2u2
Substituting u1 and u2:
A1√2gh=A2(2√gh)
Dividing both sides by √gh:
A1√2=2A2
Rearranging gives:
A2=A1√2
To make the water reach double the height, the area of the nozzle must be decreased by a factor of √2. Thus, the correct answer is (b) Decrease the area by a factor of √2.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Problems9videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Textbook Exercises)20videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Practice Problems52videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
Similar Questions
The length, breadth and height of the room are in the ratio 3:2:1. The breadth and height of the room are halved and length of the room is doubled. The area of the four walls of the room will (a) decrease by 13.64% (b) decrease by 15% (c) decrease by 18.75% (d) decrease by 30%
View SolutionFrom a pipe of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in 1 hour.
View Solution
Knowledge Check
- Question 1 - Select One
A hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2 - Question 2 - Select One
In the previous problem, the time taken to reach the maximum height will be decreased by:
A19%B5%C10%Dnone of these - Question 3 - Select One
If a height h2 of water level is further decreases then:
Acylinder will not move up and remains at original positoin.Bfor h2=H3, cylinder again starts moving upCfor h2=H4, cylinder again starts moving upDfor h2=H5, cylinder again starts moving up
Water flowing through a horizontal pipe line having a constriction. Then,
View Solution10 pipes of the same diameter can fill a tank in 24 minutes.If 2 pipes gp out of order.how long will the remaining pipe take to fill the tank?
View SolutionThe velocity of the water flowing from the inlet pipe is less than the velocity of water flowing out from the spin pipe B. Then
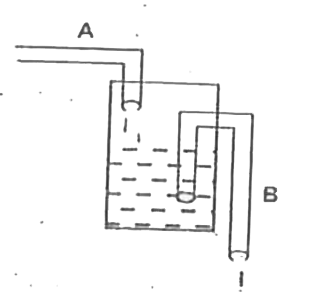 View Solution
View SolutionSuppose that water is emptied from a spherical tank of radius 10 cm. If the depth of the water in the tank is 4 cm and is decreasing at the rate of 2 cm/sec, then the radius of the top surface of water is decreasing at the rate of
View SolutionIf water falls from a tap, then the volume rate of flow of water at depth of h, (A0 is the area of cross-section of the mouth and A02 is the corresponding area at depth h)
View Solution

