If water falls from a tap, then the volume rate of flow of water at depth of h, (A0 is the area of cross-section of the mouth and A02 is the corresponding area at depth h)
A0√2gh
A0√23gh
2A0√gh
A0√3gh
The correct Answer is:B
Step by step video, text & image solution for If water falls from a tap, then the volume rate of flow of water at depth of h, (A_0 is the area of cross-section of the mouth and A_0/2 is the corresponding area at depth h) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A cylindrical container of cross-section area, A is filled up with water upto height 'h' Water may exit through a tap of cross sectional area 'a' in the bottom of container. Find out
(a) Velocity of water just after opening of tap.
(b) The area of cross-section of water stream coming out of tape at depth h0 below tap in terms of 'a' just after opening of tap.
(c) Time in which conainer becomes empty.
(Given : (aA)1/2=0.22,h=20cm,h0=20cmView SolutionThe rate of volume of flow of water (V) through a canal is found to be a function of the area of cross section A of the canal and velocity of water v. Show that the rate of volume flow is proportional to the velocity of flow of water.
View Solution
Knowledge Check
- Question 1 - Select One
Water from a tap of cross sectional area 1cm2 starts falling down vertically, with a speed of 1m/s. What is the area of cross section of the stream of water at a distance of 20cm below the mouth of the tap?
[Assume that (1) the flow is steady, (2) pressure is constant throughout the stream of water and g=10m/s2]A3×10−5m2B4×10−5m2C5×10−5m2D6×10−5m2 - Question 2 - Select One
A swimming pool, 30 m long has a depth of water of 80 cm at one end and 2.4 m the other end. Find the area of the vertical cross-section of the pool along the length.
A54 m2B48 m2C36 m2D42 m2 - Question 3 - Select One
Water from a tap emerges vertically downward with an initial speed of 3.0 m/s. The cross-sectional area of the tap is 10−4m2 . Assume that the pressure is constant throughout the stream of water and that the flow is steady. The cross-sectional area of the stream 2 m below the tap is:
A0.7×10−5m2B10−4m2C4.3×10−5m2D2.8×10−5m2
The rate of volume flow of water through a canal is found to be a function of the area of cross-section of the canal and velocity of water. Show that the rate of volume flow is proportional to the velocity of flow of water.
View Solution_E01_111_Q01.png)
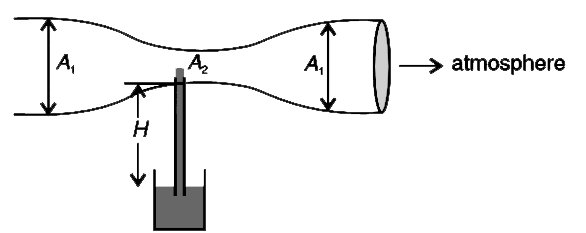
Water coming out of the mouth of a tap and falling vertically in stream line flwo forms a tapering column. i.e., the area of cross-section of the liquid column decreases as it moves down which of the following is the most accurate explanantion for this-View Solution(i) Air (density=ρ) flows through a horizontal venturi tube that discharges to the atmosphere. The area of cross section of the tube is A1 and at the constriction it is A2. The constriction is connected to a water (density=ρ0) tank through a vertical pipe of lenght H. Find the volume flow rate (Q) of the air through tube that is needed to just draw the water into the tube.
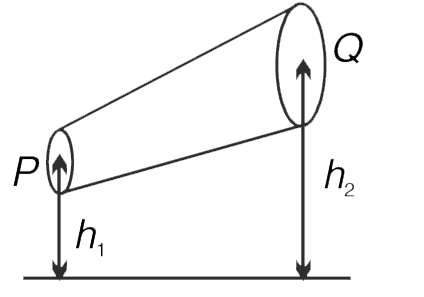
(ii) A non viscous liquid of constant density ρ flows in a stremline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross section of the tube at two points P and Q at heights of h1 and h2 are respectively A1 and A2. The velocity of the liquid at point P is v. Find the work done on a small volume ΔV of fluid by the neighbouring fluid as the small volume moves from P to Q.
View SolutionWater coming out of the mouth of a tap and falling vertically in streamline flow forms a tapering column, i.e., the area of cross-section of the liquid column decreases as it moves down. Which of the following is the most accurate explanation for this ?
.View SolutionWater flows from the base of rectangular tank of depth 16 mater. The rate of flowing the water is proportional to the square root of depth at any time t. If depth is 4 mater when t=2 hours then after 3 hours the depth is
View Solution