A wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)2
where y0=4mm,T=1.0sandλ=4cm.(a) find the velocity of wave. (b) find the function f(t) giving the displacement of particle at x=0. (c) find the function g(x) giving the shape of the string at t=0.(d) plot the shape g(x) of the string at t=0 (e) Plot of the shape of the string at t=5s.
(a). The wave equation is
y=Ae−(tT−xλ)2
This may be expressed as
y=Ae−1λ2(x−λT1)2
This is the form f(x−vt)
Therefore,the velocity of wave v=λ/T=8.0/1.0=8cm/s
(b). substituting t=0 in given Eq. (i),we get
f(t)=Ae−(t/T)2
(c ) substituting t=0 in given Eq.(i), we get
g(x)=aE(−(X/LAMBDA)2)
(d). At t=0, the displacement is maximum at the originwhile at t=5s, the displacement is maximum at distance x=vt=8×5=40cm
The function g(x) at t=0 and 5s are plotted in s−5.2 (a) and (b)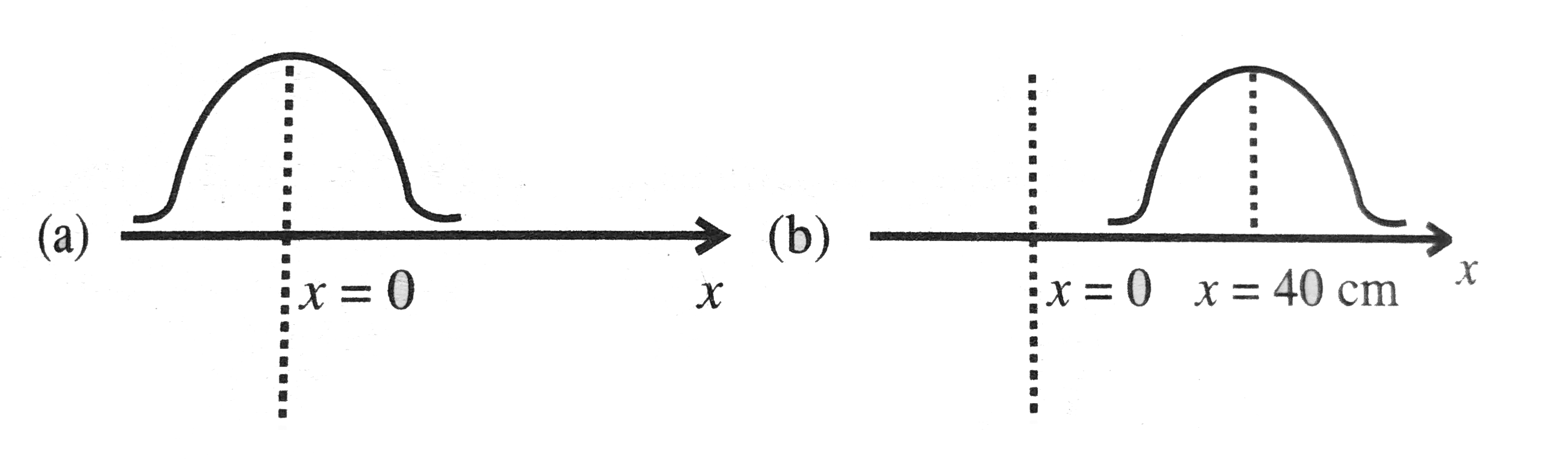
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A pulse is propagating on a long stretched string along its length taken as positive x-axis. Shape of the string at t = 0 is given by y=√a2−x2when |x|≤a=0 when |x|≥a . What is the general equation of pulse after some time 't' , if it is travelling along positive x-direction with speed V?
View SolutionThe displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given by f(t)=Asin(tT). The wave speed is v. Write the wave equation.
View SolutionA travelling wave on a long stretched string along the positIve x-axis is given by y=5mme(T5s−x5cm)2 . Using this equation answer the following questions.
The velocity of the wave is
View SolutionThe displacement of A particle at x = 0 of a stretched string carrying a wave in the positive X-direction is given by f(t)=Ae−t2. The wave speed is V. Write equation of the wave.
View SolutionA wave pulse is travelling on a string with a speed v towards the positive X-axis. The shape of the string at t = 0 is given by g(x)=Asin(xa), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time 1, if the wave speed is v.
View SolutionA travelling wave on a long stretched string along the positIve x-axis is given by y=5mme(t5s−x5cm)2. Using this equation answer the following questions.
At t = 0, x = 0, the displacement of the wave is
View SolutionTwo pulses travelling in opposite directions along a string are shown for t=0 in the figure. Plot the shape of the string at t= 1.0, 2.0, 3.0, 4.0 and 5.0s respectively .

View SolutionA wave pulse is travelling along +x direction on a string at 2m/s. Displacement y (in cm ) of the parrticle at x=0 at any time t is given by 2/(t2+1). Find
(i) expression of the function y=(x,t),i.e., displacement of a particle at position x and time t.
Draw the shape of the pulse at t=0 and t=1 s.
View SolutionA transverse wave propagating along x-axis is represented as y(x,t)=0.8sin(π4−4πt−π2x)where x is in meter and t is in second. The velocity of wave is
View SolutionA travelling wave on a long stretched string along the positIve x-axis is given by y=5mme(T5s−x5cm)2. Using this equation answer the following questions.
The plot of y and x at t = 10 s is best indicated by
View Solution
