A heavy uniform rope is held vertically and is tensioned by clamping it to a rigid support at the lower end. A wave of a certain frequency is set up at the lower end. Will the wave travel up the rope with the same speed?
To solve the problem, we need to analyze how the wave travels through the rope and how the tension in the rope affects the wave speed.
1. Understanding the Setup:
- We have a heavy uniform rope that is clamped at the lower end. This means that the lower end is fixed and cannot move. The rope is vertical, and we are interested in how a wave travels up this rope.
2. Identifying the Forces:
- At any point along the rope, the tension (T) in the rope will vary depending on the distance (x) from the lower end. The tension at the lower end is affected by the weight of the rope above that point.
3. Calculating the Mass:
- The mass of the rope segment above a point at distance x can be calculated as:
m=ML⋅x
where M is the total mass of the rope and L is its total length.
4. Applying Newton's Second Law:
- For a small segment of the rope, the net force acting on it can be expressed as:
Tx−F=m⋅g
where F is the force exerted by the clamp, and g is the acceleration due to gravity.
5. Finding the Tension:
- The tension at a distance x from the bottom can be expressed as:
Tx=F+(ML⋅x)g
This shows that the tension increases with distance x.
6. Wave Speed in the Rope:
- The speed of a wave (v) in a rope is given by the formula:
v=√Tμ
where T is the tension and μ is the linear mass density of the rope.
7. Analyzing the Wave Speed:
- Since the tension Tx increases with distance x, the wave speed will also change as it travels up the rope. Specifically, as we move up the rope, the tension increases, leading to an increase in wave speed.
8. Conclusion:
- Therefore, the wave will not travel up the rope with the same speed. The speed will increase as the wave moves upward due to the increasing tension in the rope.
Final Answer:
No, the wave will not travel up the rope with the same speed because the tension in the rope increases with distance from the lower end, leading to an increase in wave speed.
- We have a heavy uniform rope that is clamped at the lower end. This means that the lower end is fixed and cannot move. The rope is vertical, and we are interested in how a wave travels up this rope.
- At any point along the rope, the tension (T) in the rope will vary depending on the distance (x) from the lower end. The tension at the lower end is affected by the weight of the rope above that point.
- The mass of the rope segment above a point at distance x can be calculated as:
m=ML⋅x
where M is the total mass of the rope and L is its total length.
- For a small segment of the rope, the net force acting on it can be expressed as:
Tx−F=m⋅g
where F is the force exerted by the clamp, and g is the acceleration due to gravity.
- The tension at a distance x from the bottom can be expressed as:
Tx=F+(ML⋅x)g
This shows that the tension increases with distance x.
- The speed of a wave (v) in a rope is given by the formula:
v=√Tμ
where T is the tension and μ is the linear mass density of the rope.
- Since the tension Tx increases with distance x, the wave speed will also change as it travels up the rope. Specifically, as we move up the rope, the tension increases, leading to an increase in wave speed.
- Therefore, the wave will not travel up the rope with the same speed. The speed will increase as the wave moves upward due to the increasing tension in the rope.
No, the wave will not travel up the rope with the same speed because the tension in the rope increases with distance from the lower end, leading to an increase in wave speed.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Subjective16videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct62videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.19videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A heavy uniform rope is held vertically by clamping it to a rigid support at the upper end. A wave of a certain frequency is set up at the lower end. The wave will
View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionA thick uniform rope of length L is hanging from a rigid support. A transverse wave of wavelength λ0 is set up in the middle of the rope. The wavelength of the wave as it reaches the top most point is
 View Solution
View SolutionA Uniform rope having mass m hags vertically from a rigid support. A transverse wave pulse is produced at the lower end. The speed v of wave pulse varies with height h from the lower end as
View SolutionA perfectly elastic uniform string is suspended vertically with its upper end fixed to the ceiling and the lower end loaded with the weight. If a transverse wave is imparted to the lower end of the string, the pulse will
View SolutionA string is hanging from a rigid support. A transverse wave pulse is set up at the bottom. The velocity v of thr pulse related to the distance covered by it is given as
 View Solution
View SolutionA uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2
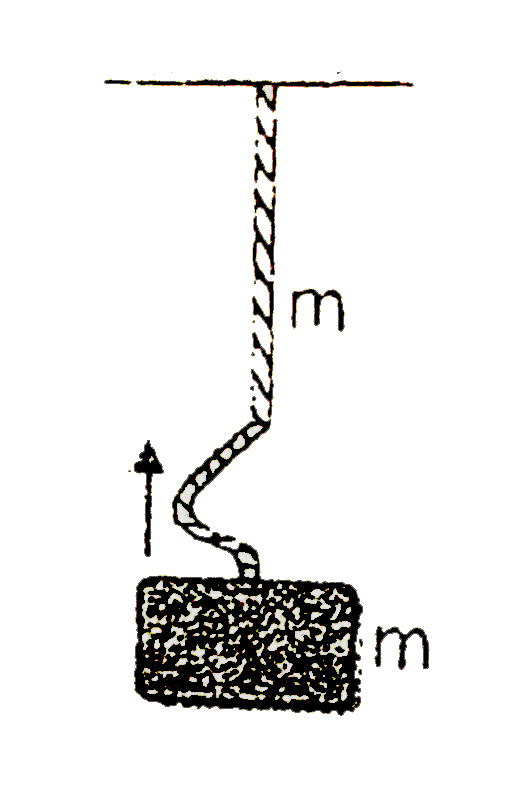 View Solution
View SolutionA chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
View SolutionA chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
View Solution

