A wave on a string is described by y(x,t)=Acos(kx−ωt). (a) Graph y,vy, and ay as function of x for time t=0. (b) consider the following points on the string: (i) x=0,(ii) x=pi//4k, (iii) x=pi//2k, (iv)x=3pi//4k, (v)x=pi//k, (vi)x=5pi//4k, (vii) x=3pi//2k, (viii) x=7pi//4k. For a particle at each of these points at t=0, describes in words whether the particle is moving and in what direction, and whether the particle is speeding up, slowing down, or instantaneously not acceleraring.
To solve the problem, we will go through the following steps:
Step 1: Determine the wave function at t=0
Given the wave equation:
y(x,t)=Acos(kx−ωt)
At t=0, the equation simplifies to:
y(x,0)=Acos(kx)
Step 2: Plot the graph of y as a function of x
The function y(x,0)=Acos(kx) is a cosine wave. The graph will oscillate between A and −A with a period of 2πk.
Step 3: Calculate the velocity vy
The velocity of the wave is given by the time derivative of the displacement:
vy=∂y∂t=∂∂t(Acos(kx−ωt))=Aωsin(kx−ωt)
At t=0:
vy(x,0)=Aωsin(kx)
Step 4: Plot the graph of vy as a function of x
The function vy(x,0)=Aωsin(kx) is a sine wave. The graph will oscillate between Aω and −Aω with a period of 2πk.
Step 5: Calculate the acceleration ay
The acceleration is given by the time derivative of the velocity:
ay=∂vy∂t=∂∂t(Aωsin(kx−ωt))=−Aω2cos(kx−ωt)
At t=0:
ay(x,0)=−Aω2cos(kx)
Step 6: Plot the graph of ay as a function of x
The function ay(x,0)=−Aω2cos(kx) is also a cosine wave, but it is inverted. The graph will oscillate between −Aω2 and Aω2 with a period of 2πk.
Step 7: Analyze the motion of particles at specified points
Now, we will analyze the motion of the particles at the specified points x=0,π4k,π2k,3π4k,πk,5π4k,3π2k,7π4k at t=0.
1. At x=0:
- y(0,0)=A
- vy(0,0)=0 (particle is at rest)
- ay(0,0)=−Aω2 (particle is accelerating downwards)
2. At x=π4k:
- y(π4k,0)=Acos(π4)=A√2
- vy(π4k,0)=Aωsin(π4)=Aω√2 (particle is moving upwards)
- ay(π4k,0)=−Aω2cos(π4)=−Aω2√2 (particle is slowing down)
3. At x=π2k:
- y(π2k,0)=0
- vy(π2k,0)=Aω (particle is moving upwards)
- ay(π2k,0)=−Aω2 (particle is accelerating downwards)
4. At x=3π4k:
- y(3π4k,0)=−A√2
- vy(3π4k,0)=Aω√2 (particle is moving upwards)
- ay(3π4k,0)=Aω2√2 (particle is speeding up)
5. At x=πk:
- y(πk,0)=−A
- vy(πk,0)=0 (particle is at rest)
- ay(πk,0)=Aω2 (particle is accelerating upwards)
6. At x=5π4k:
- y(5π4k,0)=−A√2
- vy(5π4k,0)=−Aω√2 (particle is moving downwards)
- ay(5π4k,0)=Aω2√2 (particle is speeding up)
7. At x=3π2k:
- y(3π2k,0)=0
- vy(3π2k,0)=−Aω (particle is moving downwards)
- ay(3π2k,0)=Aω2 (particle is accelerating upwards)
8. At x=7π4k:
- y(7π4k,0)=A√2
- vy(7π4k,0)=−Aω√2 (particle is moving downwards)
- ay(7π4k,0)=−Aω2√2 (particle is slowing down)
y(x,t)=Acos(kx−ωt)
At t=0, the equation simplifies to:
y(x,0)=Acos(kx)
vy=∂y∂t=∂∂t(Acos(kx−ωt))=Aωsin(kx−ωt)
At t=0:
vy(x,0)=Aωsin(kx)
ay=∂vy∂t=∂∂t(Aωsin(kx−ωt))=−Aω2cos(kx−ωt)
At t=0:
ay(x,0)=−Aω2cos(kx)
- y(0,0)=A
- vy(0,0)=0 (particle is at rest)
- ay(0,0)=−Aω2 (particle is accelerating downwards)
- y(π4k,0)=Acos(π4)=A√2
- vy(π4k,0)=Aωsin(π4)=Aω√2 (particle is moving upwards)
- ay(π4k,0)=−Aω2cos(π4)=−Aω2√2 (particle is slowing down)
- y(π2k,0)=0
- vy(π2k,0)=Aω (particle is moving upwards)
- ay(π2k,0)=−Aω2 (particle is accelerating downwards)
- y(3π4k,0)=−A√2
- vy(3π4k,0)=Aω√2 (particle is moving upwards)
- ay(3π4k,0)=Aω2√2 (particle is speeding up)
- y(πk,0)=−A
- vy(πk,0)=0 (particle is at rest)
- ay(πk,0)=Aω2 (particle is accelerating upwards)
- y(5π4k,0)=−A√2
- vy(5π4k,0)=−Aω√2 (particle is moving downwards)
- ay(5π4k,0)=Aω2√2 (particle is speeding up)
- y(3π2k,0)=0
- vy(3π2k,0)=−Aω (particle is moving downwards)
- ay(3π2k,0)=Aω2 (particle is accelerating upwards)
- y(7π4k,0)=A√2
- vy(7π4k,0)=−Aω√2 (particle is moving downwards)
- ay(7π4k,0)=−Aω2√2 (particle is slowing down)
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The angle of intersection of the curves y=2 sin2x and y=cos2 x at x=π6 is
(a)π/4
(b) π/2
(c) π/3
(d) π/6
View SolutionA xandy co-ordinates of a particle are x=Asin(ωt)andy=Asin(ωt+π/2). Then, the motion of the particle is

View SolutionThe displacement of a particle is given by x=3sin(5πt)+4cos(5πt). The amplitude of particle is
View SolutionThe angle between the tangents to the curve y=x2−5x+6 at the point (2, 0) and (3, 0) is (a)π2 (b) π3 (c) π (d) π4
View SolutionFind the values of k so that the function f is continuous at the indicated point inf(x)={kcosxπ−2xifx≠π23ifx=π2 at x=π2
View SolutionIn which of the following intervals the inequality, sinx<cosx<tanx<cotx can hold good ? (a) (7π4,2π) (b) (3π4,π) (c) (5π4,3π2) (d) (0,π4)
View SolutionIf the area of the circle 4x2+4y2−8x+16y+k=0 is 9π square units, then the value of k is
View SolutionThe solution(s) of the equation sin7x+cos2x=−2 is/are (a)x=2kπ7+3π14, k∈I (b) x=nπ+π4 k∈I x=2nπ+π2, k∈I (d) none of these
View SolutionA wave disturbance in a medium is described by Y=0.02cos(50πt+π2)cosπx . Where x and y are in m and t in sec. The values in Column-II are in SI units.
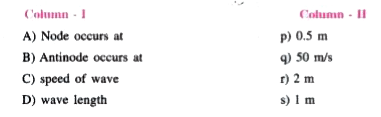
View SolutionIf sinx+cosx=√y+1y for x∈[0,π] , then (a) x=π4 (b) y=0 (c) y=1 (d) x=3π4
View Solution
