A wave on a string is described by y(x,t)=Acos(kx−ωt). (a) Graph y,vy, and ay as function of x for time t=0. (b) consider the following points on the string: (i) x=0,(ii) x=π/4k, (iii) x=π/2k, (iv)x=3π/4k, (v)x=π/k, (vi)x=5π/4k, (vii)x=3π/2k, (viii) x=7π/4k. For a particle at each of these points at t=0, describes in words whether the particle is moving and in what direction, and whether the particle is speeding up, slowing down, or instantaneously not acceleraring.
y=Asin(ωt−kx), Particle velocity
vp(X,t)=δyδt=ωAcos(omηt−kx)
and particle acceleration
ap(x,t)=δ2yδt2=−ω2Asin(ωt−kx)
i) t=0,x=0:vp=+ωAandap=0 i.e., particle is moving upwards but its acceleration is zero.
ii) At t=0,x=π4k,Vp=Aω√2, upward and
ap=ω2A√2 upward
Topper's Solved these Questions
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
5 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
13 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
Similar Questions
A xandy co-ordinates of a particle are x=Asin(ωt)andy=Asin(ωt+π/2). Then, the motion of the particle is

View SolutionThe displacement of a particle is given by x=3sin(5πt)+4cos(5πt). The amplitude of particle is
View SolutionThe angle of intersection of the curves y=2 sin2x and y=cos2 x at x=π6 is
(a)π/4
(b) π/2
(c) π/3
(d) π/6
View SolutionFind the values of k so that the function f is continuous at the indicated point inf(x)={kcosxπ−2xifx≠π23ifx=π2 at x=π2
View SolutionIf the area of the circle 4x2+4y2−8x+16y+k=0 is 9π square units, then the value of k is
View SolutionA wave disturbance in a medium is described by Y=0.02cos(50πt+π2)cosπx . Where x and y are in m and t in sec. The values in Column-II are in SI units.
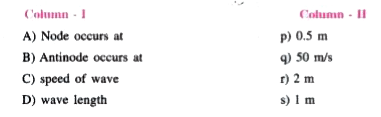
View SolutionIf sinx+cosx=√y+1y for x∈[0,π] , then (a) x=π4 (b) y=0 (c) y=1 (d) x=3π4
View SolutionIf sinx+cosx=√y+1y for x∈[0,π] , then x=π4 (b) y=0 y=1 (d) x=3π4
View SolutionThe velocity of a particle moving in the x−y plane is given by
dxdt=8πsin2πtanddydt=5πsin2πt
where, t=0,x=8andy=0, the path of the particle is.
View SolutionFor f(x)=sin2x,x∈(0,π) point of inflection is: π6 (b) 2π4 (c) 3π4 (d) 4π3
View Solution
