A wave propagates on a string in positive x-direction with a speed of 40 cm/s. The shape of string at t = 2 s is y=10cosx5 where x and y are in centimeter. The wave equation is
10cos(x5−8t+16∘), 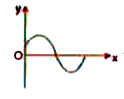
Topper's Solved these Questions
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - I)
59 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
Similar Questions
A wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given by
View SolutionA wave pulse is travelling on a string with a speed v towards the positive X-axis. The shape of the string at t = 0 is given by g(x)=Asin(xa), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time 1, if the wave speed is v.
View Solution
Knowledge Check
A wave is represented by the equation
y=Asin(10πx+15πt+π/3)
Where x is in metre and t is in second.
a wave travelling in the positive x-direction with a velocity of 1.5 m/s
a wave travelling in the negative x-direction with a velocity 1.5 m/s
a wave travelling in the negative x-direction with a wavelength of 0.2 m
a wave travelling in the positive x-direction with a wavelength 0.2 mAa wave travelling in the positive x-direction with a velocity of 1.5 m/sBa wave travelling in the negative x-direction with a velocity 1.5 m/sCa wave travelling in the negative x-direction with a wavelength of 0.2 mDa wave travelling in the positive x-direction with a wavelength 0.2 m
The displacement of a wave disturbance propagating in the positive x-direction is given by
y=11+x2at t=0 and y=11+(x−1)2 at t=2s
where, x and y are in meter. The shape of the wave disturbance does not change during the propagation. what is the velocity of the wave?
View SolutionA sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at x=2 cm is found at its mean position and it is moving in positive y-direction at t=1 s. the amplitude of the wave, the wavelength and the angular frequency of the wave are 0.1m,π/4m and 4πrad/s, respectively.
The speed of particle at x=2m and t=1s is
View SolutionA sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at x=2 cm is found at its mean position and it is moving in positive y-direction at t=1 s. the amplitude of the wave, the wavelength and the angular frequency of the wave are 0.1m,π/4m and 4πrad/s, respectively.
The equation of the wave is
View SolutionA transversee wave propagating on the string can be described by the equationy=2sin(10x+300t) , where x and y are in metres and t in second. If the vibrating string has linear density of 0.6×10−3g/cm , then the tension in the string is
View SolutionFigure shows a wave pulse at t=0. The pulse moves to the right with a speed of 10cms^-1. Sketch the shape of the string at t=1s, 2s and 3s.

View SolutionThe linear density of a vibrating string is 10−4kg/m. A transverse wave is propagating on the string, which is described by the equation y=0.02sin(x+30t), where x and y are in metres and time t in seconds. Then tension in the string is
View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
View Solution
