A wave travelling on a string at a speed of 10ms−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave ? (b) If the displacement of a particle is 1.5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant ?
The correct Answer is:A, B, C
Wave speed =v=10msec
Timeperiod=T=20ms
=20×10−32×10−2sec
a. Wavelength λ=vt=10×2×10−2
=0.02m=20cm
b. wavelengthλ=20cm
∴Phased⇔erence=((2pi)/lamda).x<br>=((2pi)/20)xx10=pirad<br>y_1=asin(omegat-kx)<br>rarr 1.5=asin(omegat-kx)<br>So,thedisplacementofthepartic≤∗diatancex=10cm
=[ϕ=2πxλ=2π×1020=π] is given by
y2=asin(ωt−kx+π)
=asin(ωt−kx)=1.5mm
:. displacement =1.5mm
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -29videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer9videos
THE FORCES
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
Similar Questions
At two particular closest instant of time t1 and t2 the displacements of a particle performing SHM are equal. At these instant
View SolutionOcean waves of time period 10 s have wave velocity 15 ms−1. Find the wavelength of these waves .
View SolutionA sinusoidal wave is traveling on a string with speed 40 cm/s. The displacement of the particle of the string at x = 10 cm varies with time according to
y = (5.0cm) sin(1.0−4.0s−1)t)The linear density of the string is 4.0 g/cmView SolutionA particle of mass 1031kg is moving with a velocity equal to 105ms−1. The wavelength of the particle is equal to
View SolutionA sine wave is travelling in a medium. A particular partile has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
View SolutionIn the diagram shown, a particle is moving from the point A to the point B. Length of each arrow is 1 m and the particle is moving at a constant speed of 1ms−1 . What is the displacement of the particle?
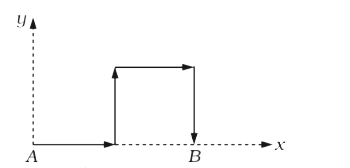 View Solution
View SolutionA particle simple harmonic motion completes 1200 oscillations per minute and passes through the mean position with a velocity 3.14ms−1. Determine displacement of the particle from its mean position. Also obtain the displacement equation of the particle if its displacement be zero at the instant t=0.
View SolutionA long string having a cross- sectional area 0.80mm2 and density 12.5gcm−3 is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (b) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (c) What is the velocity of this particle at this instant ?
View SolutionA wave travels along the positive x-direction with a speed of 20ms−1. The amplitude of the wave is 0.20 cm and the wavelength 2.0 cm. (a) Write a suitable wave equation which describes this wave. (b) What is the displacement and velocity of the particle at x = 2.0 cm at time t = 0 according to the wave equation written ?
View SolutionA transverse waves is travelling in a string. Study following statement.
(i) Equation of the wave is equal to the shape of the string at an instant t. (ii) Equation of thhe wave is general equation for displacement of a particle of the string (iii) Equation of the wave must be sinusoidal equation (iv) Equation of the wave is an equation for displacement of the particle at one end only.correct statement areView Solution

