A wedge of mass M is kept at rest on smooth surface a particle of mass m hits the wedge normally. Find the velocity of wedge and particle just after collision. Take coefficient of restitution as e.
To solve the problem of a wedge of mass M on a smooth surface colliding with a particle of mass m, we will use the principles of conservation of momentum and the coefficient of restitution. Here’s a step-by-step breakdown of the solution:
Step 1: Define the Initial Conditions
- Let the initial velocity of the particle be v0.
- The wedge is initially at rest, so its initial velocity is 0.
- The angle of inclination of the wedge is θ.
Step 2: Analyze the Collision
- After the collision, let the velocity of the wedge be V and the velocity of the particle be vn.
- The particle hits the wedge normally, and we need to consider the components of the velocities in the horizontal direction.
Step 3: Apply Conservation of Momentum
- The momentum before the collision in the horizontal direction is given by:
pinitial=mv0sinθ
- After the collision, the momentum is:
pfinal=MV+mvnsinθ
- By conservation of momentum:
mv0sinθ=MV+mvnsinθ(1)
Step 4: Apply the Coefficient of Restitution
- The coefficient of restitution e relates the velocities before and after the collision:
e=Velocity of separationVelocity of approach
- The velocity of approach is v0 (the particle's velocity towards the wedge), and the velocity of separation is Vsinθ−vn:
Vsinθ−vn=ev0(2)
Step 5: Solve Equations (1) and (2)
- From equation (2), we can express vn:
vn=Vsinθ−ev0
- Substitute vn into equation (1):
mv0sinθ=MV+m(Vsinθ−ev0)
- Rearranging gives:
mv0sinθ=MV+mVsinθ−mev0
- Combine like terms:
mv0sinθ+mev0=MV+mVsinθ
- Factor out V:
(M+msinθ)V=mv0(1+e)sinθ
- Solve for V:
V=mv0(1+e)sinθM+msinθ(3)
Step 6: Substitute V to Find vn
- Now substitute V back into the expression for vn:
vn=(mv0(1+e)sinθM+msinθ)sinθ−ev0
- Simplifying gives:
vn=mv0(1+e)sin2θM+msinθ−ev0
Final Results
- The velocities after the collision are:
V=mv0(1+e)sinθM+msinθ
vn=mv0(1+e)sin2θM+msinθ−ev0
- Let the initial velocity of the particle be v0.
- The wedge is initially at rest, so its initial velocity is 0.
- The angle of inclination of the wedge is θ.
- After the collision, let the velocity of the wedge be V and the velocity of the particle be vn.
- The particle hits the wedge normally, and we need to consider the components of the velocities in the horizontal direction.
- The momentum before the collision in the horizontal direction is given by:
pinitial=mv0sinθ
- After the collision, the momentum is:
pfinal=MV+mvnsinθ
- By conservation of momentum:
mv0sinθ=MV+mvnsinθ(1)
- The coefficient of restitution e relates the velocities before and after the collision:
e=Velocity of separationVelocity of approach
- The velocity of approach is v0 (the particle's velocity towards the wedge), and the velocity of separation is Vsinθ−vn:
Vsinθ−vn=ev0(2)
- From equation (2), we can express vn:
vn=Vsinθ−ev0
- Substitute vn into equation (1):
mv0sinθ=MV+m(Vsinθ−ev0)
- Rearranging gives:
mv0sinθ=MV+mVsinθ−mev0
- Combine like terms:
mv0sinθ+mev0=MV+mVsinθ
- Factor out V:
(M+msinθ)V=mv0(1+e)sinθ
- Solve for V:
V=mv0(1+e)sinθM+msinθ(3)
- Now substitute V back into the expression for vn:
vn=(mv0(1+e)sinθM+msinθ)sinθ−ev0
- Simplifying gives:
vn=mv0(1+e)sin2θM+msinθ−ev0
- The velocities after the collision are:
V=mv0(1+e)sinθM+msinθ
vn=mv0(1+e)sin2θM+msinθ−ev0
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A particle of mass m collides with another stationary particle of mass M such that the second particle starts moving and the first particle stops just after the collision. Then which of the following conditions must always be valid ?
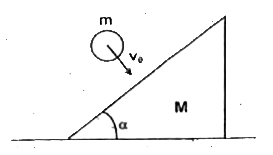
View SolutionA wedge of mass M and angle α rests on a smooth horizontal plane. A smooth sphere of mass m strickes it in a direction perpendicular to its inclined face and rebounds. If the coefficient of restitution is e, find the ratio of the speed of the sphere just before and just after the impact.
View SolutionA wedge of mass M lies on a smooth fixed wedge of inclination θ. A particle of mass m lies on the wedge of mass M in the figure. All surfaces are frictionless and the distance of the block from the fixed wedge is l. Find.
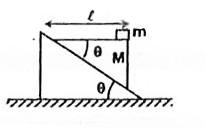
(a) Normal reaction between m and M
(b) the time after which the particle will hit the fixed plane.
View SolutionA wedge of mass M=4m lies on a frictionless plane. A particle of mass m approaches the wedge with speed v. there is no friction between the particle and the plane or between the particle and the wedge. The maximum height climbed by the particle on the wedge is given by
View SolutionA wedge of mass M = 4m lies on a frictionless plane. A particle of mass m approaches the wedge with speed v. There is no friction between the particle and the plane or between the particle and the wedge. The maximum height climbed by the particle on the wedge is given by:
View SolutionA smooth ball of mass 1kg is projected with velocity 7m/s horizontal from a tower of height 3.5m. It collides elastically with a wedge of mass 3 kg and inclination of 45∘ kept on ground. The ball collides with the wedge at a height of 1m above the ground. Find the velocity of the wedge and the ball after collision. (Neglect friction at any contact.)

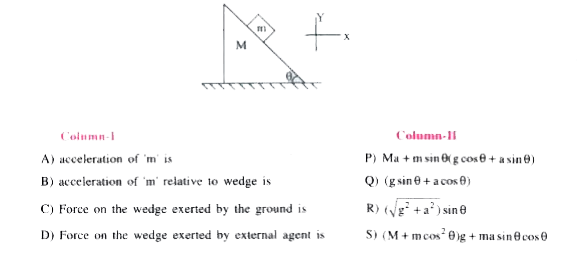
View SolutionA block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
View SolutionA small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. If h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
View SolutionA particle (a mud pallet, say) of mass m strikes a smooth stationary wedge of mass M with as velocity v0 at an angle θ with horizontal. If the collision is perfectly inelastic, find the
a. velocity of the wedge just after the collision.
b. Change in KE of the system (M+m) in collision.
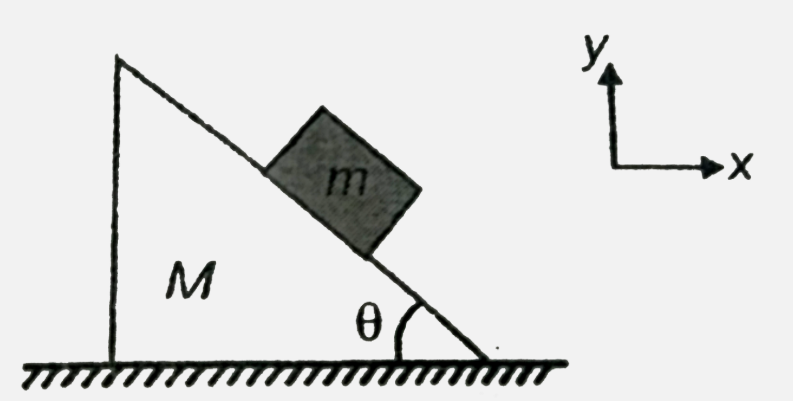
View SolutionA block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View Solution
