A weightless spring of length 60 cm and force constant 200Nm−1 is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
π20s
π10s
π5s
π√200s
The correct Answer is:B
Given : k=1000N/m
When a mass of 0.25 kg is attached at the middle of spring, it will work as the combination of two equal springs in parallel, each of spring constant
k.=2k=2×100=200N/m
The equivalent spring constant is
keq=k.+k.=200+200=400N/m
∴ Time period, T=2π√Mkeq=2π√0.25400=π20s
Topper's Solved these Questions
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - CHECK YOUR NEET VITALS
25 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ
14 Videos
Similar Questions
A spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionA spring is stretched by 5cm by a force 10N. The time period of the oscillations when a mass of 2Kg is suspended by it is
View Solution
Knowledge Check
A weightless spring of length 60 cm and force constant 200 N/m is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
Aπ20sBπ10sCπ5sDπ√200sA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3KmA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A 1 kg mass is attached to a spring of force constant 600 N/m and rests on a smooth horizontal surface with other end of the spring tied to wall as shown in figure. A second mass of 0.5 kg slides along the surface towards the first at 3m/s. If the masses make a perfectly inelastic collision, then find amplitude and time period of oscillation of combined mass.

View SolutionA body of mass m is suspended from vertical spring and is set into simple harmonic oscillations of time period T. Next the spring is fixed at one end on a smooth horizontal table and same body is attached at the other end. The body is pulled slightly and then released to produce horizontal oscillations of the spring. The time period of horizontal oscillations is
View SolutionA load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
View SolutionThree springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
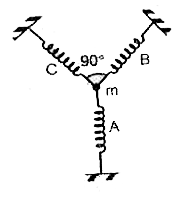
View SolutionA rod of mass m and length L is kept on a horizontal smooth surface. The rod is hinged at its one end A. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant k is rigidly attached to the lower end of rod and spring of spring constant 12k just touches the rod at its midpoint C, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small osciallation of the rod will be

View Solution
