A wheel has a radius 10 cm and it is coupled by a belt to another wheel of radius 30 cm. The smaller wheel increases its speed from rest at a uniform rate of rad/ sec. After how much time will the speed of larger wheel become 100 c.p.m. ?
2s
5s
10s
20s
The correct Answer is:C
Here, r1ω=r2ω2,r1=10cm. r2=30cm.
Also ω2=2π×10060=10π3=rads−1
ω1=r2ω2r1=3010×10π3=10πrads−1.
Using ω1=ω0+a,t. we get 10π=0+πt or t=10secconds.
Topper's Solved these Questions
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Recent Competitive Questions
3 Videos
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Revision Test
57 Videos
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Multiple Choice Questions(LEVEL II )
1 Videos
- TRANSFERENCE OF HEAT BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Recent Competitive Questions
4 Videos
- UNIT TEST -06BOOK - MODERN PUBLICATIONCHAPTER - UNIT TEST -06EXERCISE - Multiple Choice Questions
19 Videos
Similar Questions
In figure wheel A of radius rA=10cm is coupled by belt B to wheel C of radius rC=25cm. The angular speed of wheel A is increased from rest at a constant rate of 1.6rad/s2. Find the time needed for wheel C to reach an angular speed of 12.8rad/s, assuming the belt does not slip.
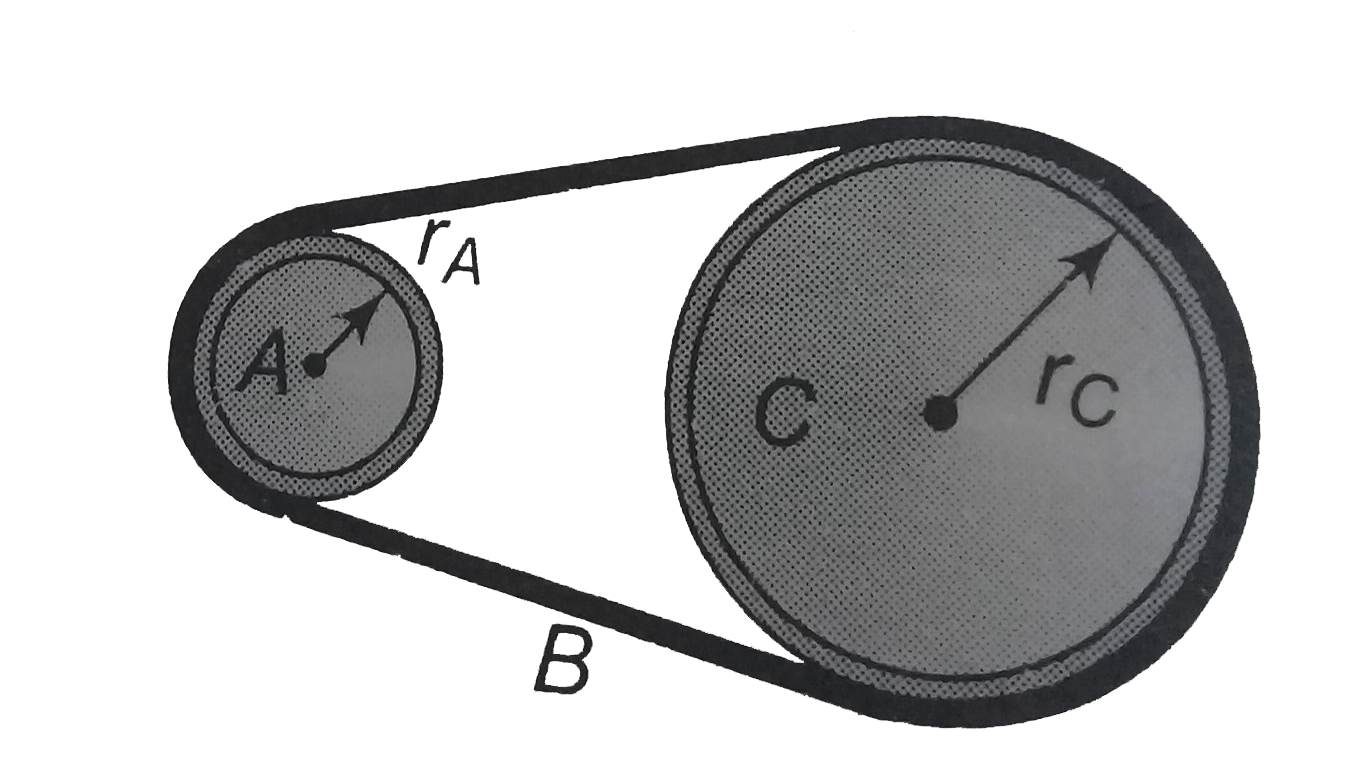 .
.
View SolutionIn Fig. 10-54, wheel A of radius rA=10cm is coupled by belt B to wheel C of radius rC=25cm. The angular speed of wheel A is increased from rest at a constant rate of 2.0rad/s2. Find the time needed for wheel C to reach an angular speed of 100 rev/min, assuming the belt does not slip.

View Solution
Knowledge Check
A wheel having radius 10 cm is coupled by a belt to another wheel of radius 30 cm . 1st wheel increases its angular speed from rest at a uniform rate of 1.5rads−2 . The time for 2nd wheel to reach a rotational speed of 100rev/min is ... (assume that the belt does not slip )
A20 secB10 secC1.5 secD15secA belt passes over a wheel of radius 25 cm. If a point on the belt has a speed of 5m/s, the belt is moving with an angular velocity of
A3.2rad/sB0.32rad/sC20rad/sD0.032rad/s
Wheel A of radius rA=10cm is coupled by a belt C to another wheel of radius rB=25cm as in the figure. The wheels are free to rotate and the belt does not slip . At time t=0 wheel A increases it's angular speed from rest at a uniform rate π/2rad/sec2 Find the time in which wheel B attains a speed of 100r±[ Hint :vA=vB]

View SolutionWheel A of radius rA=10cm is coupled by a belt C to another wheel of radius rB=25cm as in the figure. The wheels are free to rotate and the belt does not slip . At time t=0 wheel A increases it's angular speed from rest at a uniform rate π/2rad/sec2 Find the time in which wheel B attains a speed of 100r±[ Hint :vA=vB]

View SolutionTwo wheels having radii in the ratio 1:3 are connected by a common belt. If the smaller wheel is accelerated from rest at a rate 1.5rads2 for 10 s, find the angular velocity of bigger wheel
View SolutionCalculate the angular speed of againt wheel of radius 10 m, moving with a speed of 10m/s.
View SolutionFigure 10-55 shows an early method of measuring the speed of light that makes use of a rotating slotted wheel. A beam of light passes through one of the slots at the outside edge of the wheel, travels to a distant mirror, and returns to the wheel just in time to pass through the next slot in the wheel. One such slotted wheel has a radius of 5.0 cm and 500 slots around its edge. Measurements taken when the mirror is L = 500 m from the wheel indicate a speed of light of 3.0×105km/s. (a) What is the (constant) angular speed of the wheel? (b) What is the linear speed of a point on the edge of the wheel?
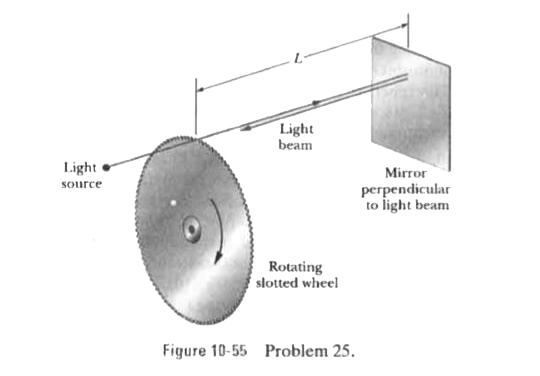
View SolutionA toothed wheel of diameter 50 cm is attached to a smaller wheel of diameter 30 cm. How many revolutions will the smaller wheel make when the larger one makes 15 revolutions?
View Solution
