Wheel A of radius rA=10cm is coupled by a belt C to another wheel of radius rB=25cm as in the figure. The wheels are free to rotate and the belt does not slip . At time t=0 wheel A increases it's angular speed from rest at a uniform rate π/2rad/sec2 Find the time in which wheel B attains a speed of 100r±[ Hint :vA=vB]
![Wheel A of radius r(A)=10cm is coupled by a belt C to another wheel of radius r(B)=25 cm as in the figure. The wheels are free to rotate and the belt does not slip . At time t=0 wheel A increases it's angular speed from rest at a uniform rate pi//2 rad //sec^(2) Find the time in which wheel B attains a speed of 100 rpm [ Hint : v(A)=v(B)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_PHY_DPP_69_XI_E01_558_Q01.png)
The correct Answer is:50/3sec.
For no slipping condition
rAαA=rBαB
⇒αB=rArBαA=1025×π2=π5rad/s2
ωB=2π×10060=10π3rad/s
ωB=ωBO+αBt
10π3=0+π5t⇒t=503sec
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 707videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 718videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 687videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
In Fig. 10-54, wheel A of radius rA=10cm is coupled by belt B to wheel C of radius rC=25cm. The angular speed of wheel A is increased from rest at a constant rate of 2.0rad/s2. Find the time needed for wheel C to reach an angular speed of 100 rev/min, assuming the belt does not slip.
 View Solution
View SolutionTwo wheels having radii in the ratio 1:3 are connected by a common belt. If the smaller wheel is accelerated from rest at a rate 1.5rads2 for 10 s, find the angular velocity of bigger wheel
View Solution
Knowledge Check
- Question 1 - Select One
A wheel having radius 10 cm is coupled by a belt to another wheel of radius 30 cm . 1st wheel increases its angular speed from rest at a uniform rate of 1.5rads−2 . The time for 2nd wheel to reach a rotational speed of 100rev/min is ... (assume that the belt does not slip )
A20 secB10 secC1.5 secD15sec - Question 2 - Select One
In figure whell A of radius rA=10cm is coupled by belt B to whell C of radius rC=25cm. The angular speed of whell A is increased from rest at a constant rate of 1.6rad/s2. Find the time needed for whell C to reach an angular speed of 12.8rad/s, assuming the belt does not slip.
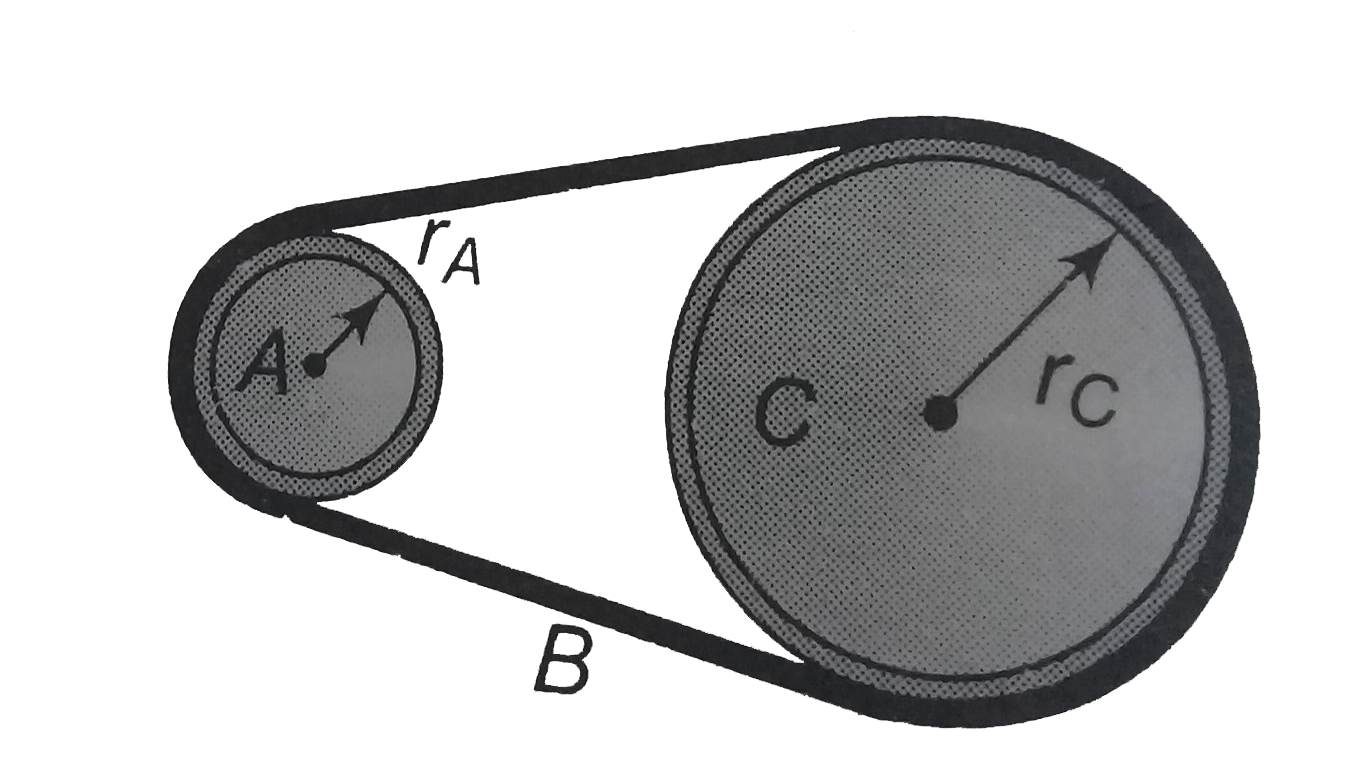 .A15 sB12.5 sC20 sD10 s
.A15 sB12.5 sC20 sD10 s - Question 3 - Select One
A belt passes over a wheel of radius 25 cm. If a point on the belt has a speed of 5m/s, the belt is moving with an angular velocity of
A3.2rad/sB0.32rad/sC20rad/sD0.032rad/s
A wheel of radius 0.1 m (wheel A) is attached by a non-stretching belt to a wheel of radius 0.2 m (wheel B). The belt does not slip. By the time wheel B turn through 1 revolution, wheel A will rotate through:
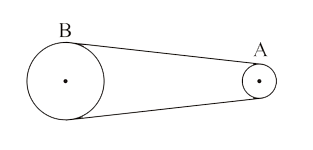 View Solution
View SolutionA wheel increases its speed from 60 rpm to 120 rpm in 10 s. Number of rotation made by it in 10 s is
View SolutionA flywheel of moment of inertia I is rotating with uniform angular speed ω. If a torque τ retards the wheel, then the time in which the wheel comes to rest is
View SolutionTwo wheels are connected by a belt. The radius of larger wheel is three times that of the smaller one . What is the ratio of the rational inertia of larger wheel to the smaller wheel , when both wheels to the same angular momentum ?
View SolutionA strap is passing over a wheel of radius 30 cm. During the time the wheel moving with initial constant velocity of 2 rev/sec. comes to rest the strap covers a distance of 25 m. The deceleration of the wheel in rad/s is
View Solution

