A wheel of mass 8 kg has moment of inertia equals to 0.5kg-m2. Determine its radius of gyration.
To determine the radius of gyration of the wheel, we can follow these steps:
Step 1: Understand the relationship between moment of inertia, mass, and radius of gyration.
The moment of inertia (I) of a body can be expressed in terms of its mass (m) and radius of gyration (k) using the formula:
I=m⋅k2
Step 2: Rearrange the formula to solve for the radius of gyration (k).
To find the radius of gyration, we can rearrange the formula:
k2=Im
Taking the square root of both sides gives us:
k=√Im
Step 3: Substitute the given values into the formula.
We are given:
- Moment of inertia, I=0.5kg m2
- Mass, m=8kg
Now, substituting these values into the equation for k:
k=√0.5kg m28kg
Step 4: Calculate the value inside the square root.
Calculating the fraction:
0.58=0.0625
Step 5: Take the square root to find k.
Now, taking the square root:
k=√0.0625=0.25m
Step 6: Convert to centimeters if necessary.
To express this in centimeters:
k=0.25m=25cm
Final Answer:
The radius of gyration k is 0.25m or 25cm.
---
The moment of inertia (I) of a body can be expressed in terms of its mass (m) and radius of gyration (k) using the formula:
I=m⋅k2
To find the radius of gyration, we can rearrange the formula:
k2=Im
Taking the square root of both sides gives us:
k=√Im
We are given:
- Moment of inertia, I=0.5kg m2
- Mass, m=8kg
k=√0.5kg m28kg
Calculating the fraction:
0.58=0.0625
Now, taking the square root:
k=√0.0625=0.25m
To express this in centimeters:
k=0.25m=25cm
The radius of gyration k is 0.25m or 25cm.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A bicycle wheel of radius 0.3 m has a rim of mass 1.0 kg and 50 spokes, each of mass 0.01 kg. What is its moment of inertia about its axis of rotation ?
View SolutionA wheel having moment of inertia 2kg-m2 about its vertical axis, rotates at the rate of 60 rpm about this axis. The torque which can stop the wheel's rotation in one minute would be
View SolutionThe rotational kinetic energy of a disc is 450 J and its moment of inertia is 100 kg m2. What is its angular momentum ?
View SolutionIn the following figure r1 and r2 are 5cm and 30cm repectively. If the moment of inertia of wheel is 5100kgm2 then its angular acceleration will be :−

View SolutionThe moment of inertia of a solid sphere about an axis passing through the centre radius is 25MR2 , then its radius of gyration about a parallel axis t a distance 2R from first axis is
View SolutionA wheel of moment of inertia 0.500kg−m2 and radius 20.0 cm is rotating about its axis at an angular speed of 20.0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
View SolutionA wheel having moment of inertia 2kgm2 about its vertical axis, rotates at the rate of 60r± about this axis. The torque which can stop the wheel's rotation in one minute would be
View SolutionA wheel having moment of inertia 4 kg m2 about its axis, rotates at rate of 240 rpm about it. The torque which can stop the rotation of the wheel in one minute is :-
View SolutionA fixed pulley of radius 20 cm and moment of inertia 0.32 kg.m2 about its axle has a massless cord wrapped around its rim. A mass M of 2 kg is attached to the end of the cord. The pulley can rotate about its axis without any friction. The acceleration of the mass M is :- (Assuming g=10m/s2)

View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
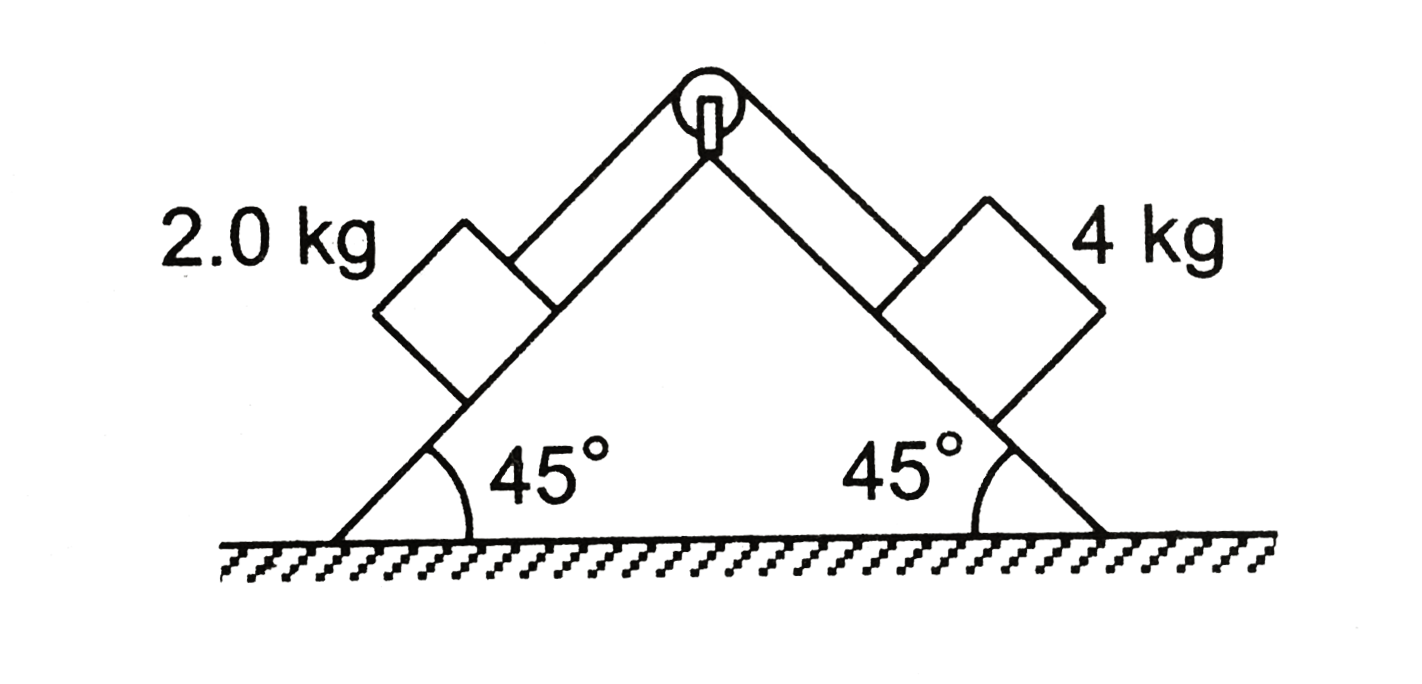
View Solution
