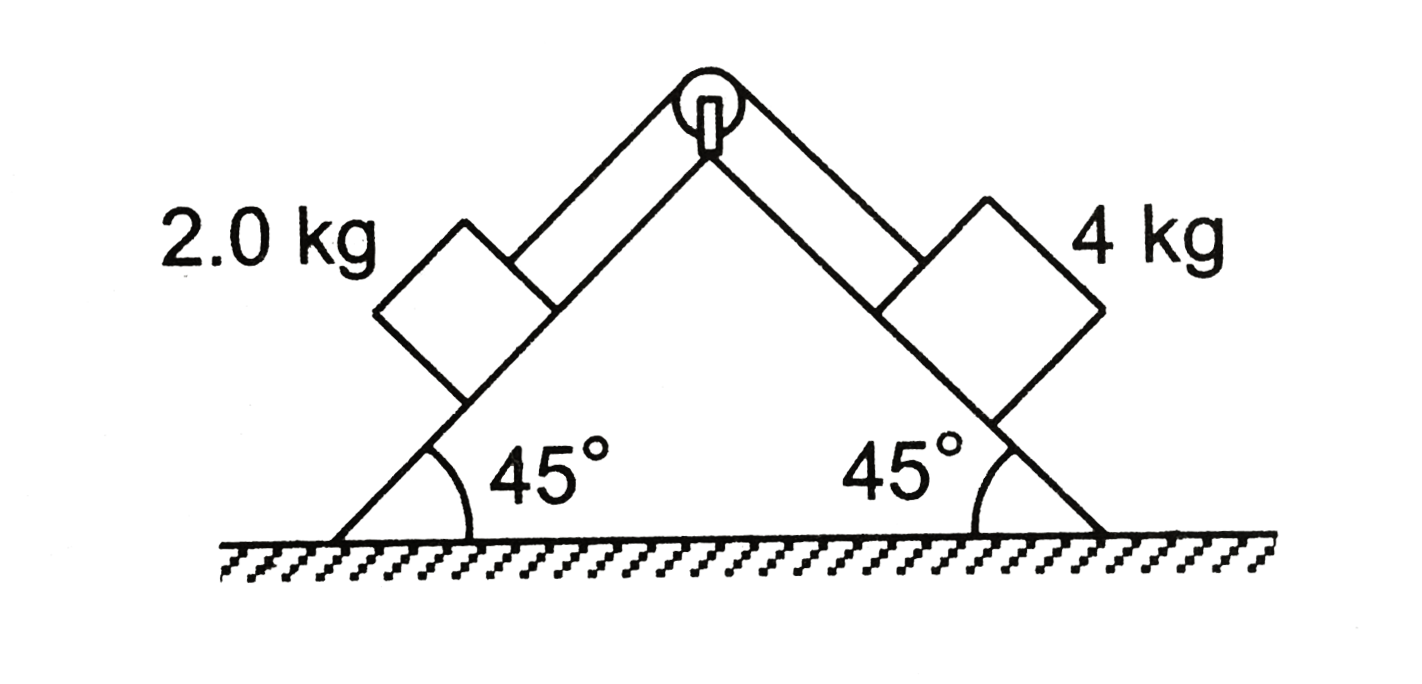
The pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
The correct Answer is:B
m1gsinθ−T1=m1a…….1
T1−T2=Iar2…..2
T2−m2gsinθ=m2a…….3
Adding the equation 1 and 3 we will get
m1gsinθ+(T2−T1)−m2gsinθ
=(m1+m2)a
→(m1−m2)gsinθ
=(m1+m2+Ir2)a
→a=(m1−m2)gsinθ(m1+m2+Ir2)
=(4−2)×10×(1√2){(4+2)+(0.50.01)}
=(2×10×1√2)6+50
=0.248=0.25ms2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Objective -2
Explore 14 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Question for short Answer
Explore 13 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Question for short Answer
Explore 15 Videos
Similar Questions
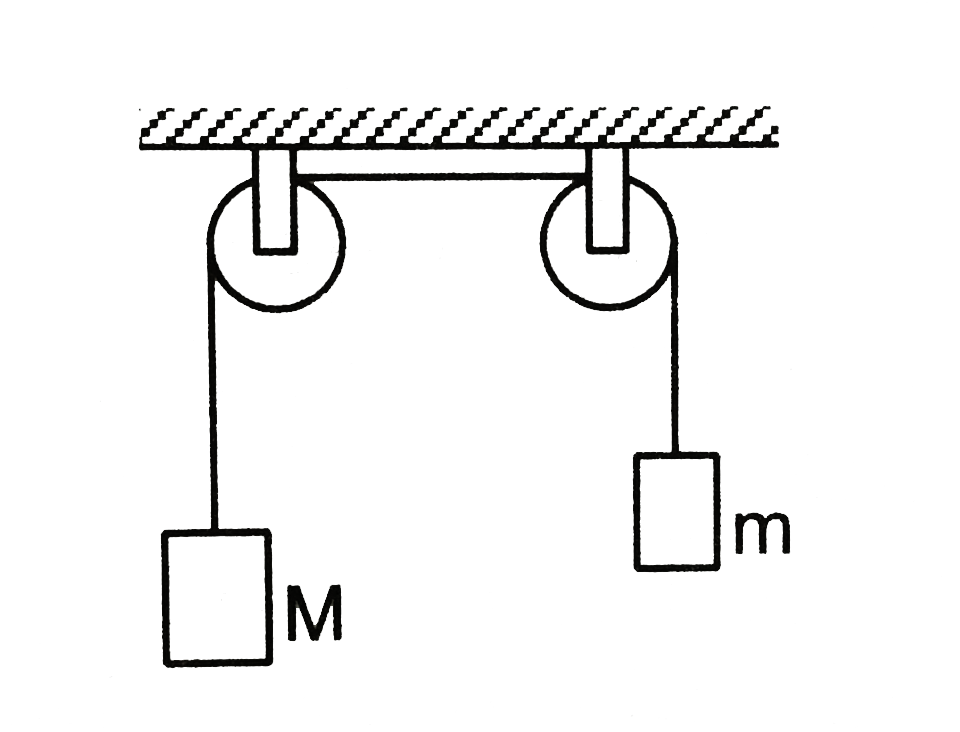
The pulleys in figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
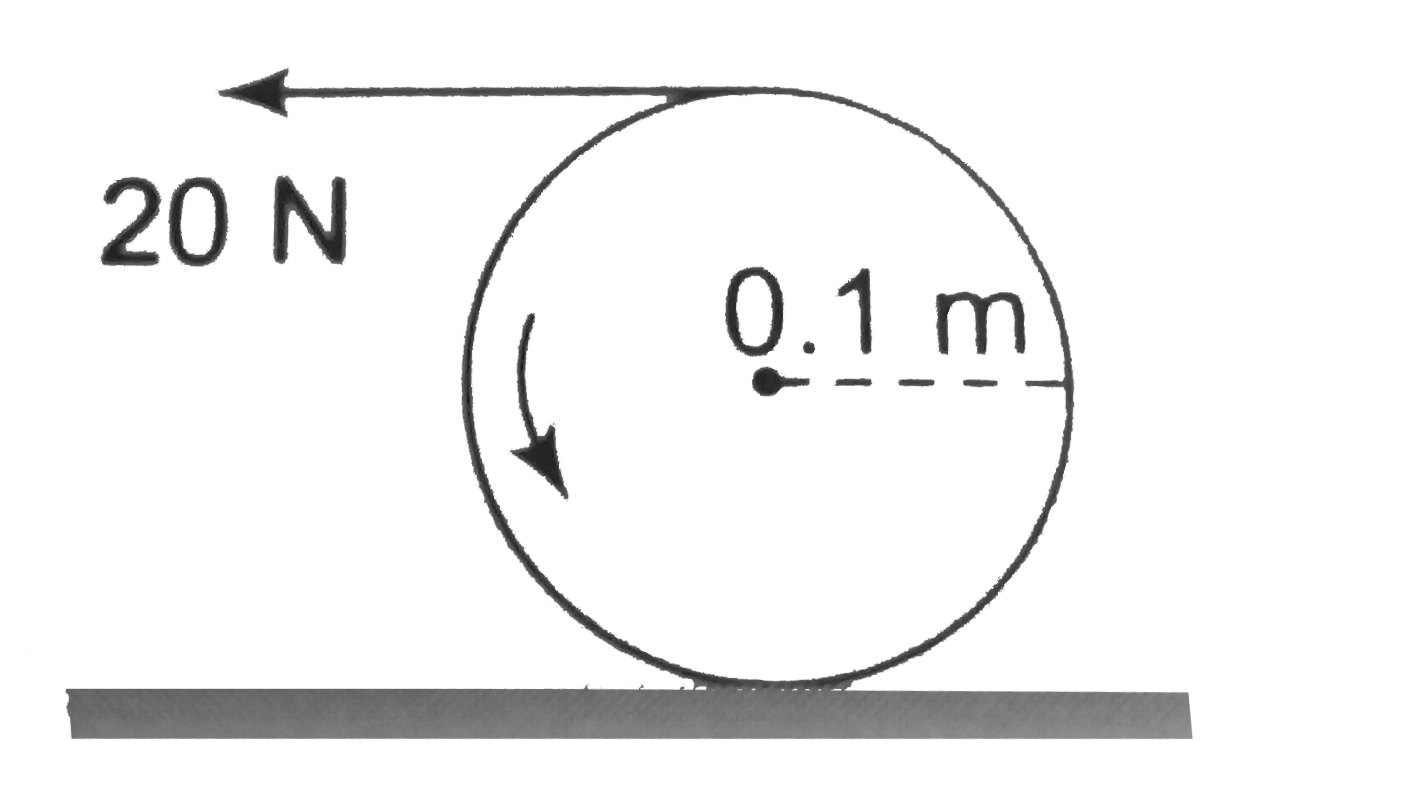
View SolutionThe rope shown in figure is wound around a cylinder of mass 4kg and moment of inertia 0.02kgm2 about the cylinder axis. If the cylinder rolls without slipping, then the linear acceleration of its centre of mass is.
 .
.
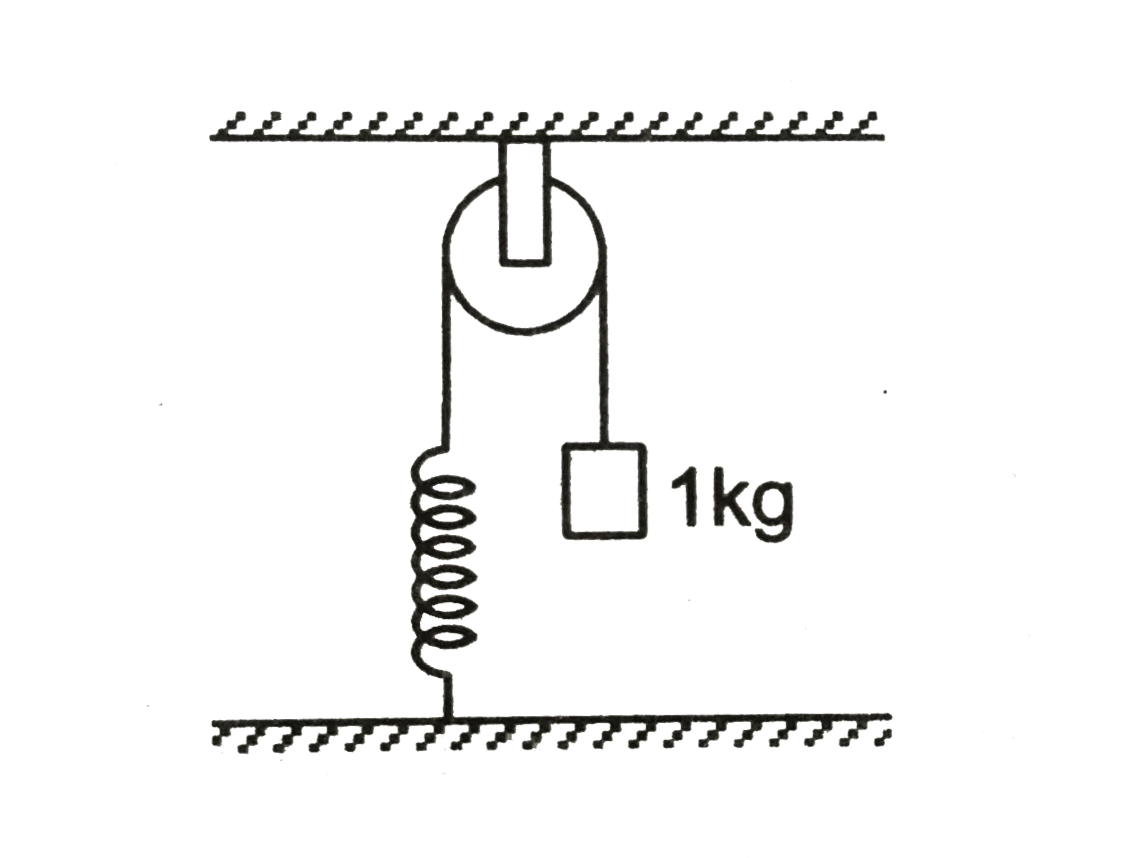
View SolutionThe pulley shown in figure has a radius of 20 cm and moment of inertial 0.2 kg-m^2. The string going over it is attached at one end to a vertical sprign of spring constant 50 N/m fixed from below and supports a 1 kg mas at other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has desceds through 10 cm. Take g=10ms2.
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
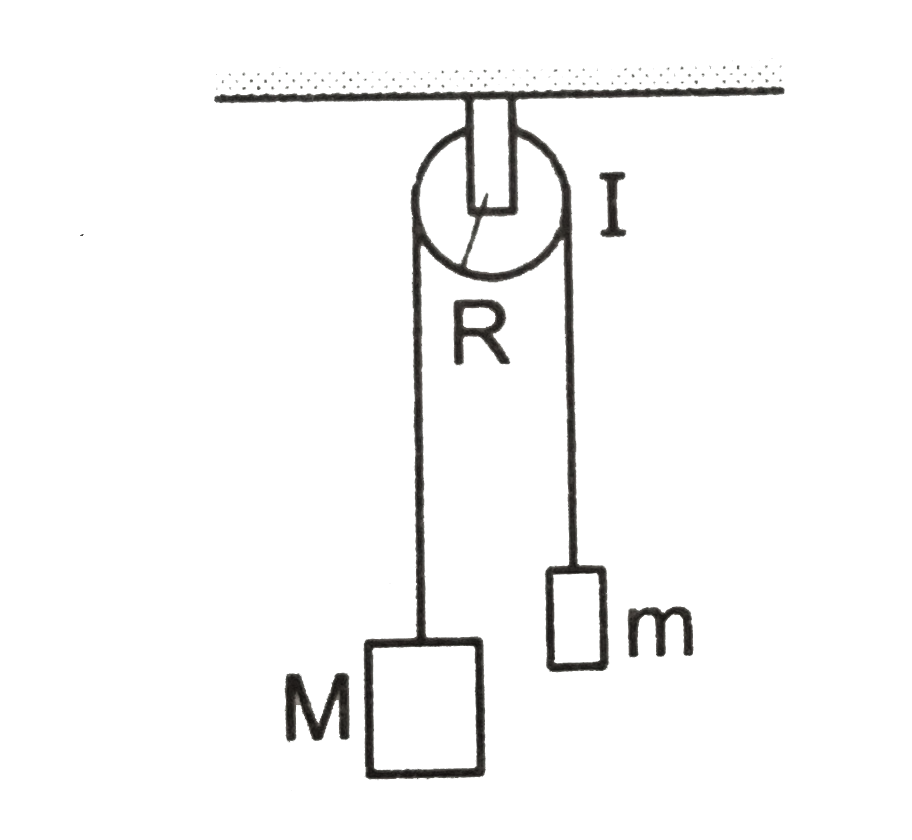
View SolutionThe pulleys in figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.

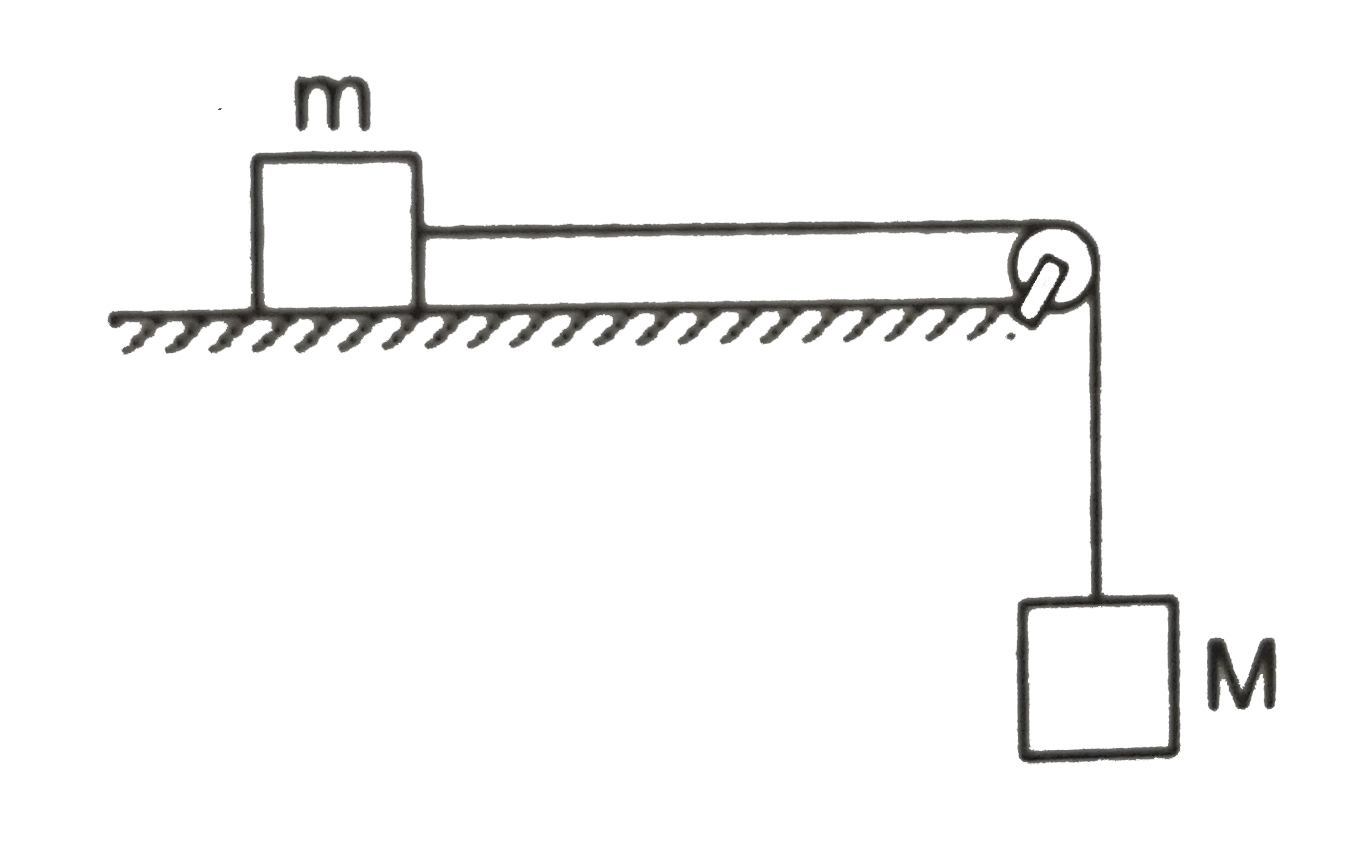
View SolutionFigure shows two blocks of masses m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.
View Solution
A small pulley of radius 20 cm and moment of inertia 0.32kg−m2 is used to hang a 2 kg mass with the help of massless string. If the block is released, for no slipping condition acceleration of the block will be
View SolutionA fixed pulley of radius 20 cm and moment of inertia 0.32 kg.m2 about its axle has a massless cord wrapped around its rim. A mass M of 2 kg is attached to the end of the cord. The pulley can rotate about its axis without any friction. The acceleration of the mass M is :- (Assuming g=10m/s2)

View Solution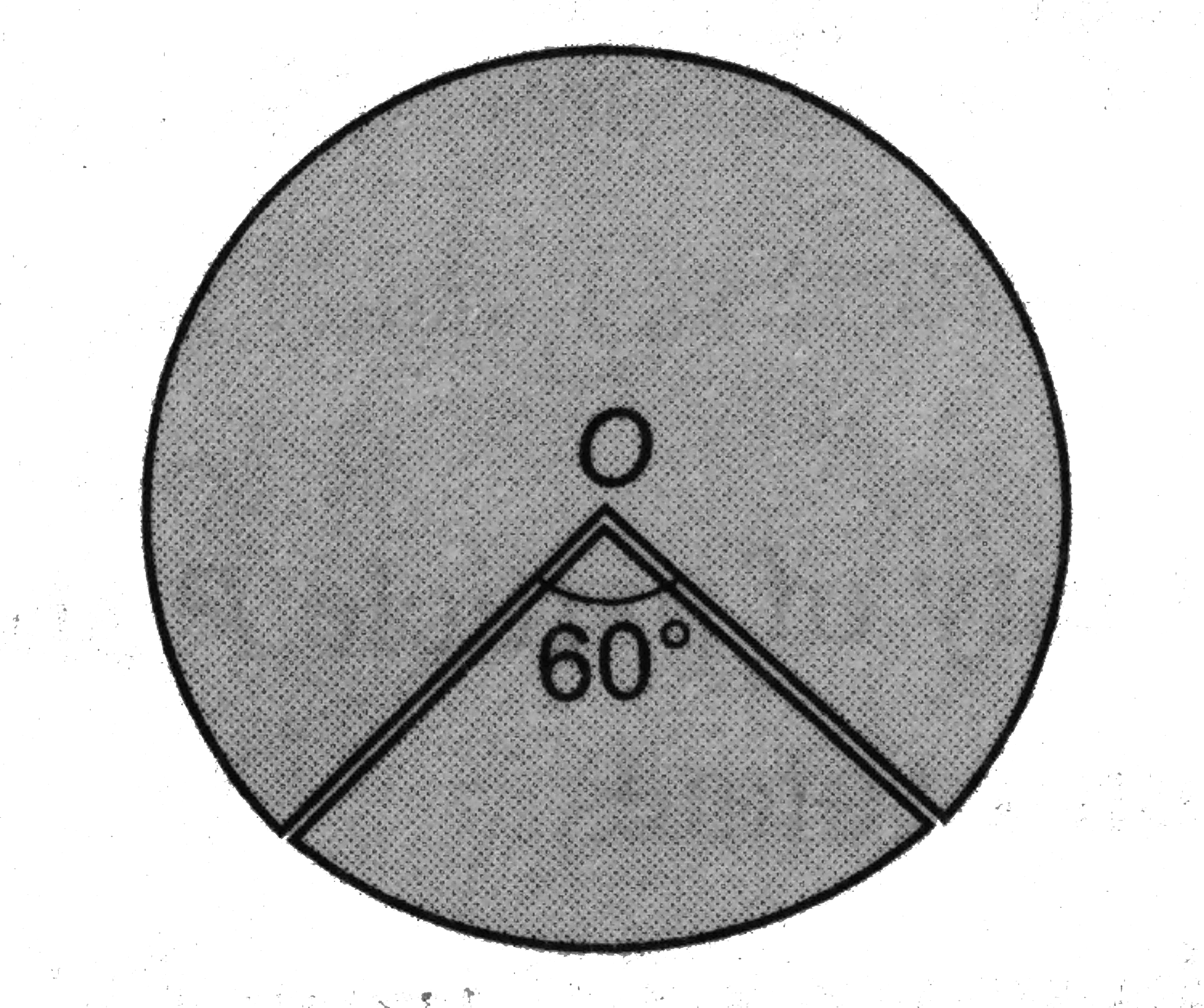
The uniform disc shown in the figure has a moment of inertia of 0.6kg−m2 around the axis that passes through O and is perpendicular to the plane of the page. If a segment is cut out from the disc as shown, what is the moment of inertia of the remaining disc?
View SolutionA solid cylinder of mass 20kg has length 1 m and radius 0.2 m. Then its moment of inertia (in kg-m2) about its geometrical axis is :
View Solution
