A wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
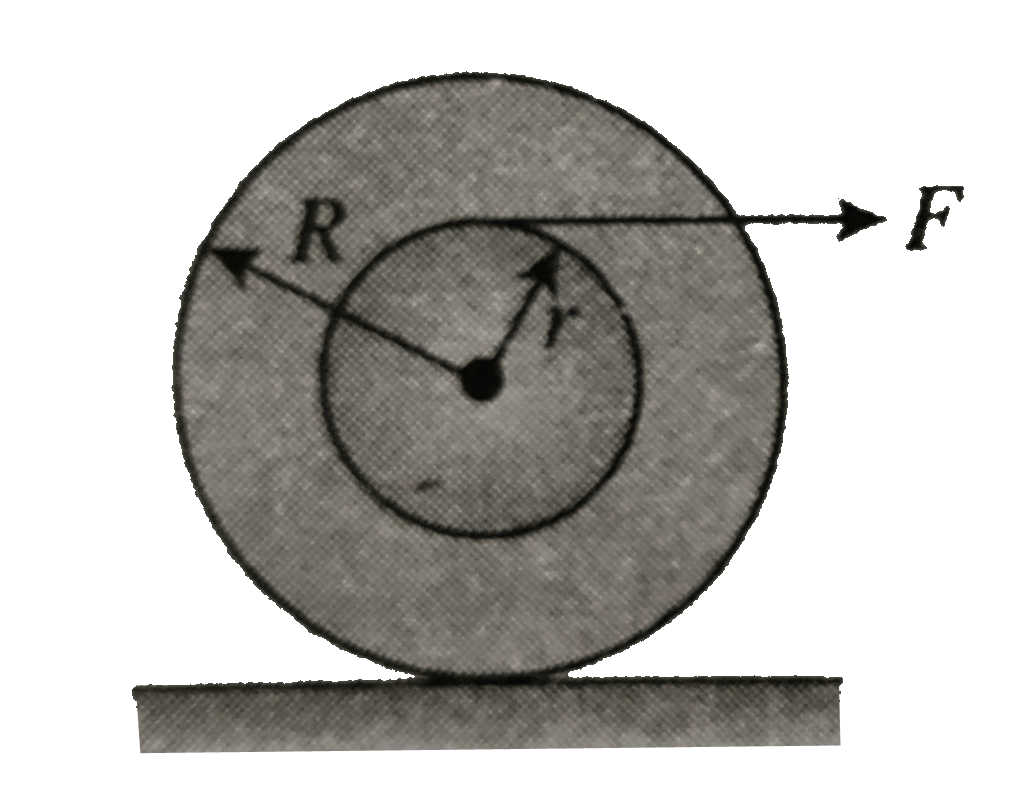
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
Step by step video & image solution for A wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel. a. What is the linear acceleration of the wheel? b. Calculate the frictional force that acts on the wheel. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE
83 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE
41 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching
3 Videos
- UNIT AND DIMENSIONSBOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem
4 Videos
Similar Questions
Consider the situation as shown in the figure. The moment of inertia of wheel is 2kgm2 and its radius is 0.25m. Find the angular acceleration of the wheel, assuming no slipping.

View SolutionA cotton reel of mass m, radius R and moment of inertia I is kept on a smooth horizontal surface. If the string is pulled horizontally by a force F, find the (i) acceleration of CM, (ii) angular acceleration of the cotton reel.

View Solution
Knowledge Check
A wheel of radius R, mass m with an axle of radius r is placed on a horizontal surface. Its moment of inertia is I=mR2. Unwinding a rope from its axel a force F is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling (∠θ=0∘)

Find the linear acceleration of the wheelAF[I/m−Rr][(I/m)+r2]B2F[(I/m)−Rr][(1/m)+r2]CF[(2I/m)−√2Rr][(I/m)+r2]DF[(I√2/m)−Rr][(I/m)+r2]A wheel of radius R, mass m with an axle of radius r is placed on a horizontal surface. Its moment of inertia is I=mR2. Unwinding a rope from its axel a force F is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling (∠θ=0∘)

Find the condition for which frictional force acts in backward directionA(I/m)>RrB(2I/m)>RrC(I√2m)>RrD(Im√2)>RrA wheel of radius R, mass m with an axle of radius r is placed on a horizontal surface. Its moment of inertia is I=mR2. Unwinding a rope from its axel a force F is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling (∠θ=0∘)

Find the condition for which frictional force acts in forward directionA(I/m)>RrB(2I/m)>RrC(I√2m)>RrD(Im√2)>Rr
A wheel of radius 20 cm is pushed ot move it on a rough horizontal surface. It is found to move through a distance of 60 cm on the road during the time it completes one revolutionabout the centre. Assume that the linear and the angular accelerations are uniform. The frictional force acting on the wheel by the surface is
View SolutionA disc of radius R and mass M is under pure rolling under the action of a force F applied at the topmost point as shown in figure. There is sufficient friciton between the disc and the horizontal surface. The acceleration is given as

View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionA wheel of radius r and mass m stands in front of a step of height h. The least horizontal force which should be applied to the axle of the wheel to allow it to raise onto the step is

View SolutionA block of mass 2 m is pulled along a horizontal frictionless surface by a rope of mass m as shown in the figure given. What force is exerted by the rope on the block ?

View Solution
