Consider the situation as shown in the figure. The moment of inertia of wheel is and its radius is . Find the angular acceleration of the wheel, assuming no slipping.


For block: ()
For pulley: ()
()
Topper's Solved these Questions
Similar Questions
The pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
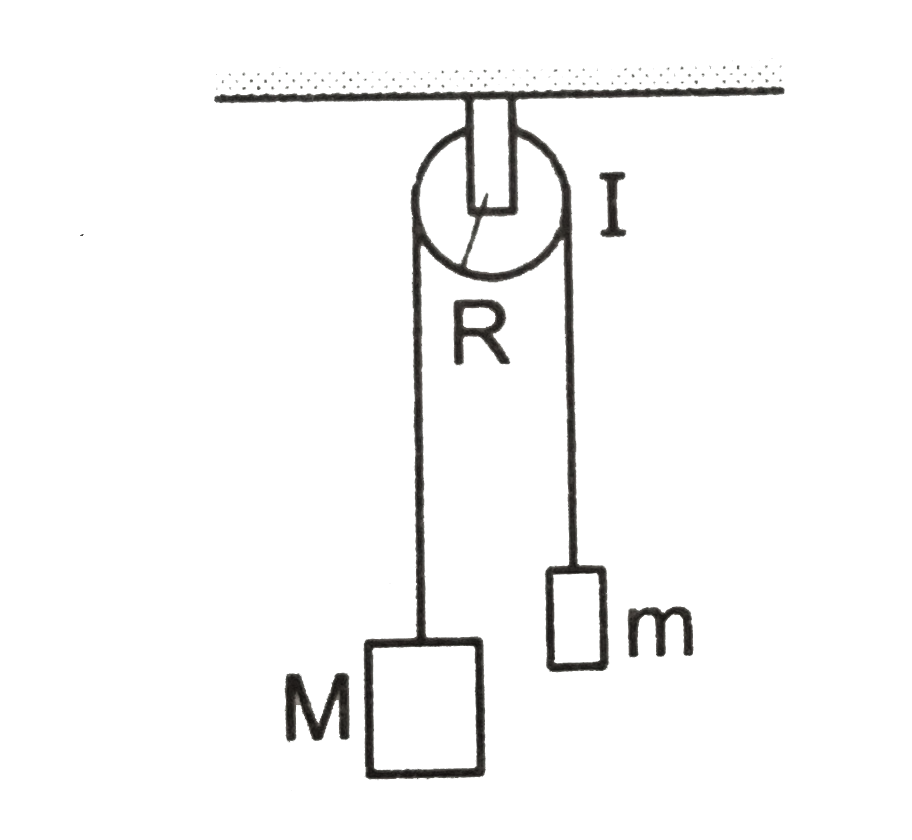 View Solution
View SolutionConsider the situation as shown. The pulley has a moment of inertia I, and radius r, the block is in equilibrium. Find the time period of mass m. Assume no slipping.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the following figure r1 and r2 are 5cm and 30cm repectively. If the moment of inertia of wheel is 5100kgm2 then its angular acceleration will be :−
 A10−4rad/s2B10−3rad/s2C10−2rad/s2D10−1rad/s2
A10−4rad/s2B10−3rad/s2C10−2rad/s2D10−1rad/s2 - Question 2 - Select One
The angular velocity of a wheel is 70rad/sec . If the radius of the wheel is 0.5 m , then linear velocity of the wheel is
A70m/sB35m/sC30m/sD20m/s - Question 3 - Select One
The fly wheel of a motor has a moment of inertia of 90 kg−m2. If the motor produces a constant torque of 270 N-m, then the angular acceleration produced in the fly wheel.
A3 rad/s2B6 rad/s2C9 rad/s2D12 rad/s2
The moment of inertia of a body is 2.5kgm2. Calculate the torque required to produce an angular acceleration of 18rads−2 in the body.
View SolutionA wheel of mass 8 kg has moment of inertia equals to 0.5kg-m2. Determine its radius of gyration.
View SolutionA wheel having moment of inertia 2 kig m^2 about its xis, rotates at 50 rpm about this axis. Find the torque that can stop the wheel in one minute.
View SolutionConsider the situation as shown in the figure. If m1>m2, I is the moment of intertia about its axis of rotation, R is the radius of pulley. The objects are released from rest separated by a vertical distance 2h. Find the translational speed of the objects as they pass each other. Assume no slipping.
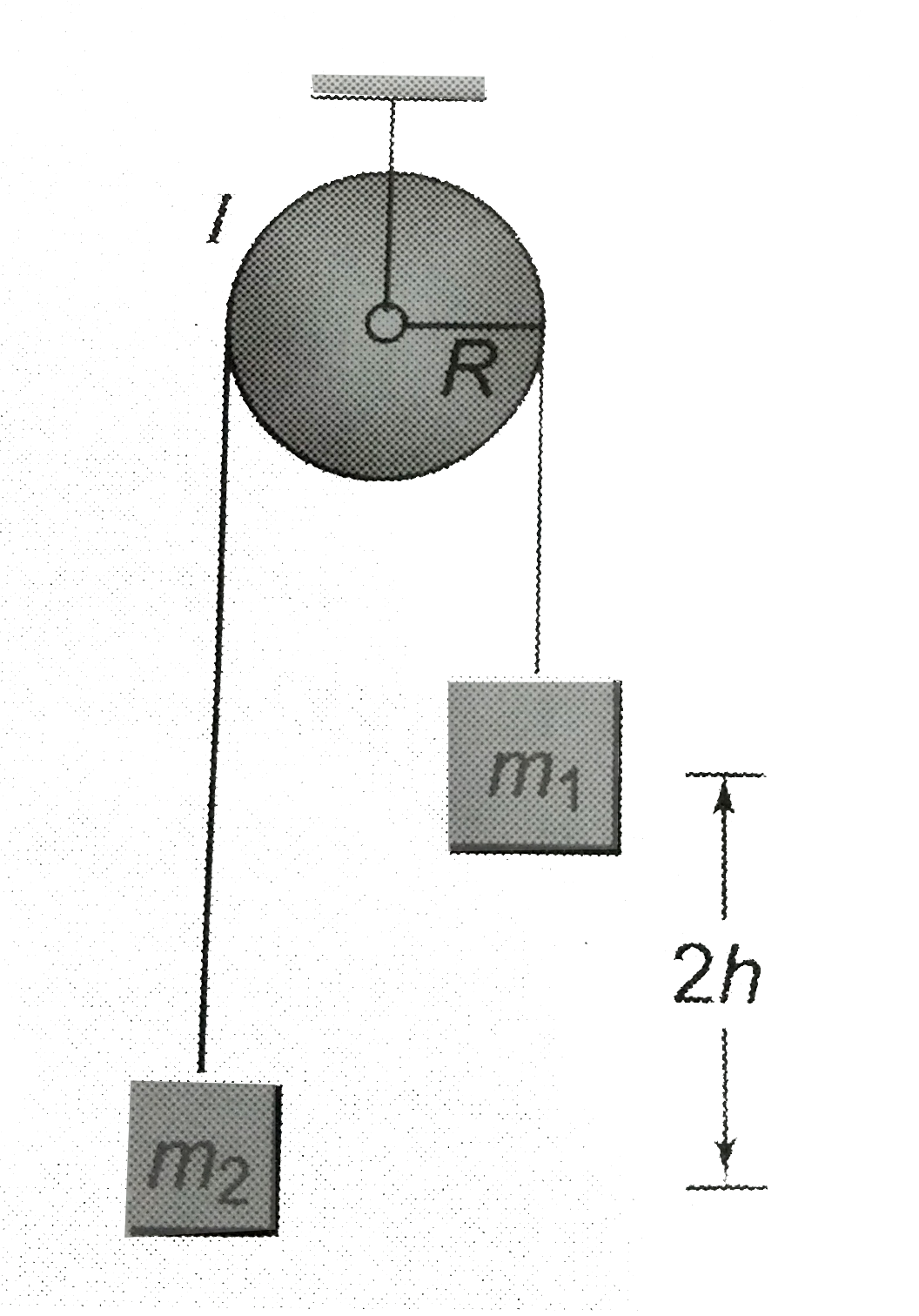 View Solution
View SolutionA wheel of mass 15 kg has a moment of inertia of 200 kg m2 about its own axis, the radius of gyration will be
View Solution

