A whitle of frequency 540 Hz rotates in a horizontal circle of radius 2 m at an angular speed of 15rads. What is the lowest and the highest frequency heard by a listener a long distance away at rest with respect to the centre of the circle? (Velocity of sound in air is c=330ms.)
To solve the problem, we will use the Doppler effect formula for sound waves. The frequency heard by an observer can change depending on the motion of the source relative to the observer.
Given Data:
- Frequency of the whistle (f) = 540 Hz
- Angular speed (ω) = 15 rad/s
- Radius of the circle (r) = 2 m
- Velocity of sound in air (c) = 330 m/s
Step 1: Calculate the linear speed of the source
The linear speed (v_s) of the source can be calculated using the formula:
vs=ω×r
Substituting the values:
vs=15rad/s×2m=30m/s
Step 2: Calculate the minimum frequency heard by the observer
The minimum frequency occurs when the source is moving away from the observer. The Doppler effect formula for frequency when the source is moving away is:
fmin=f(cc+vs)
Substituting the values:
fmin=540Hz(330330+30)
fmin=540Hz(330360)
fmin=540Hz(1112)
fmin=495Hz
Step 3: Calculate the maximum frequency heard by the observer
The maximum frequency occurs when the source is moving towards the observer. The Doppler effect formula for frequency when the source is moving towards the observer is:
fmax=f(cc−vs)
Substituting the values:
fmax=540Hz(330330−30)
fmax=540Hz(330300)
fmax=540Hz(1110)
fmax=594Hz
Final Answer:
- Minimum frequency heard by the observer: 495 Hz
- Maximum frequency heard by the observer: 594 Hz
- Frequency of the whistle (f) = 540 Hz
- Angular speed (ω) = 15 rad/s
- Radius of the circle (r) = 2 m
- Velocity of sound in air (c) = 330 m/s
The linear speed (v_s) of the source can be calculated using the formula:
vs=ω×r
vs=15rad/s×2m=30m/s
The minimum frequency occurs when the source is moving away from the observer. The Doppler effect formula for frequency when the source is moving away is:
fmin=f(cc+vs)
fmin=540Hz(330330+30)
fmin=540Hz(330360)
fmin=540Hz(1112)
fmin=495Hz
The maximum frequency occurs when the source is moving towards the observer. The Doppler effect formula for frequency when the source is moving towards the observer is:
fmax=f(cc−vs)
fmax=540Hz(330330−30)
fmax=540Hz(330300)
fmax=540Hz(1110)
fmax=594Hz
- Minimum frequency heard by the observer: 495 Hz
- Maximum frequency heard by the observer: 594 Hz
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective
56 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Single Correct
252 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.1
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
A whistle of frequency 500 Hz is rotated in a circle of radius cne metre with an angular speed of 10 radian/sec. Calculate the lowest and the highest frequency heard by a listener at a long distance away at rest with respect to the centre of the circle ? (Velocity of sound = 340m/s)
View SolutionA whistle of frequency 540 Hz is moving in a circle of radius 2 ft at a constant angular speed of 15 rad/s. What are the lowest and highest frequencies heard by a listener standing at rest, a long distance away from the centre of the circle? (Velocity of sound in air is 1100ft/s)
View SolutionA whistle of frequency 540HZ rotates in a circle of radius 2mat a linear speed of 30m/s . What is the lowest and highest frequency heard by an observer a long distance away at rest with respect to the centre of circle ? Take speed of sound of sound in air as 330m/s. Can the apparent frequency be ever equal to actual ?
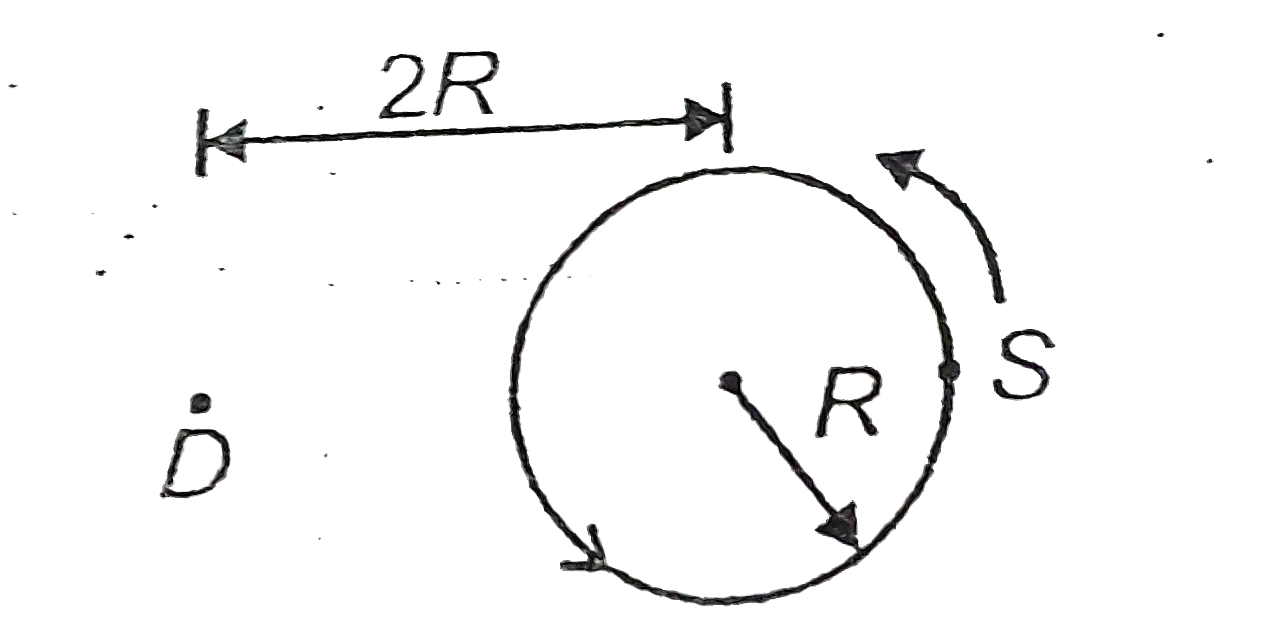
View SolutionA whistle 'S' of frequency v revolves in a circle of radius R at a constant speed v. what is the ratio of the largest and smallest frequency detected by a detector D, at rest, at a distance 2 R from the centre of the circle as shown in the figure? (take speed of sound in air as c)
View SolutionThe ratio of the apparent frequencies of a car when approaching and receding a stationary observer is 11:9 What is the speed of the car, if the velocity of sound in air is 330 m/s?
View SolutionA thunder tap is heard 5.5 s after the lightening flash. The distance of the flash is (velocity of sound in air is 330 m/s) :-
View SolutionA whistle emitting a sound of frequency 440Hz is tied to a string of 1.5m length and roated with an angular velocity of 20rad/s in the horizontal plane. Calculate the range of frequencies heard by an observer stationed at a larger distance from the whistle .(Speed of sound =330m/s) .
View SolutionA small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 1002π cm at a constant angular speed of 5-0 revolutions per second. A listener situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air =332ms−1.
View SolutionA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer who is at rest at a great distance from the centre of the circle but nearly in the same plane, the minimum fmin and the maximum fmax of the range of values of the apparent frequency heard by him will be
View SolutionA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer who is at rest at a great distance from the centre of the circle but nearly in the same plane, the minimum fmin and the maximum fmax of the range of values of the apparent frequency heard by him will be
View Solution
