A wire is bent into three segments each of radius r. Each segment is a quardant of a circle. The first segment lies in X−Y plane, the second in the Y−Z plane and third in XZ plane. If a current i flows in the wire then net dipole moment of wire is:
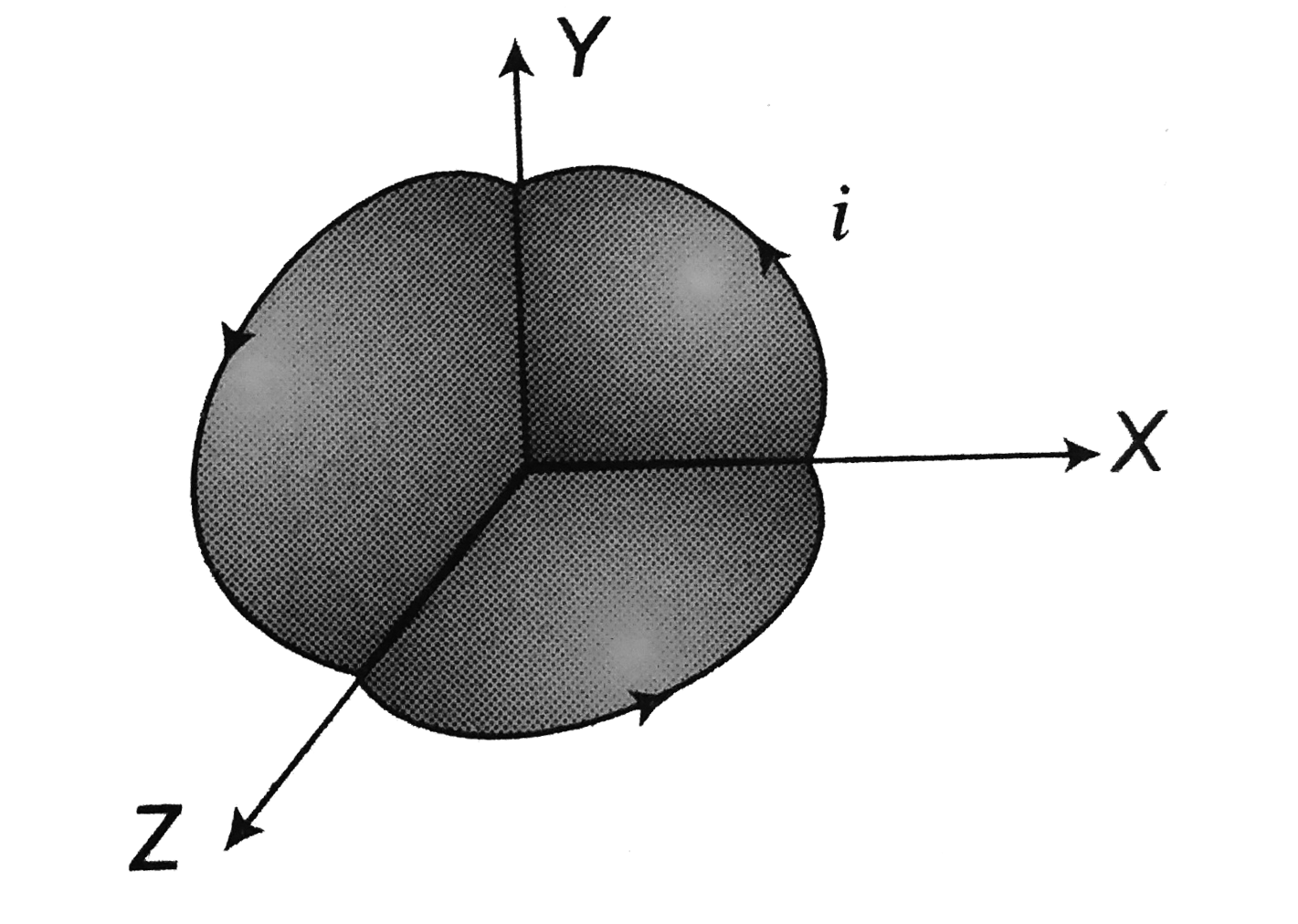
πa2i(ˆi+ˆj)
πa24i(ˆi+ˆj+ˆk)
πa22i(ˆj+ˆk)
πa22i(ˆi+ˆj+ˆk)
The correct Answer is:B
The circular segments in each of the quadrants can be considered individually for calculating the magnetic magnet. Thus, segments in each of the quadrants are considered as loops individual by joining the two ends hypothetically in the same plane. When all the three segments are considered together, the contribution by hypothetical elements are cancelled.
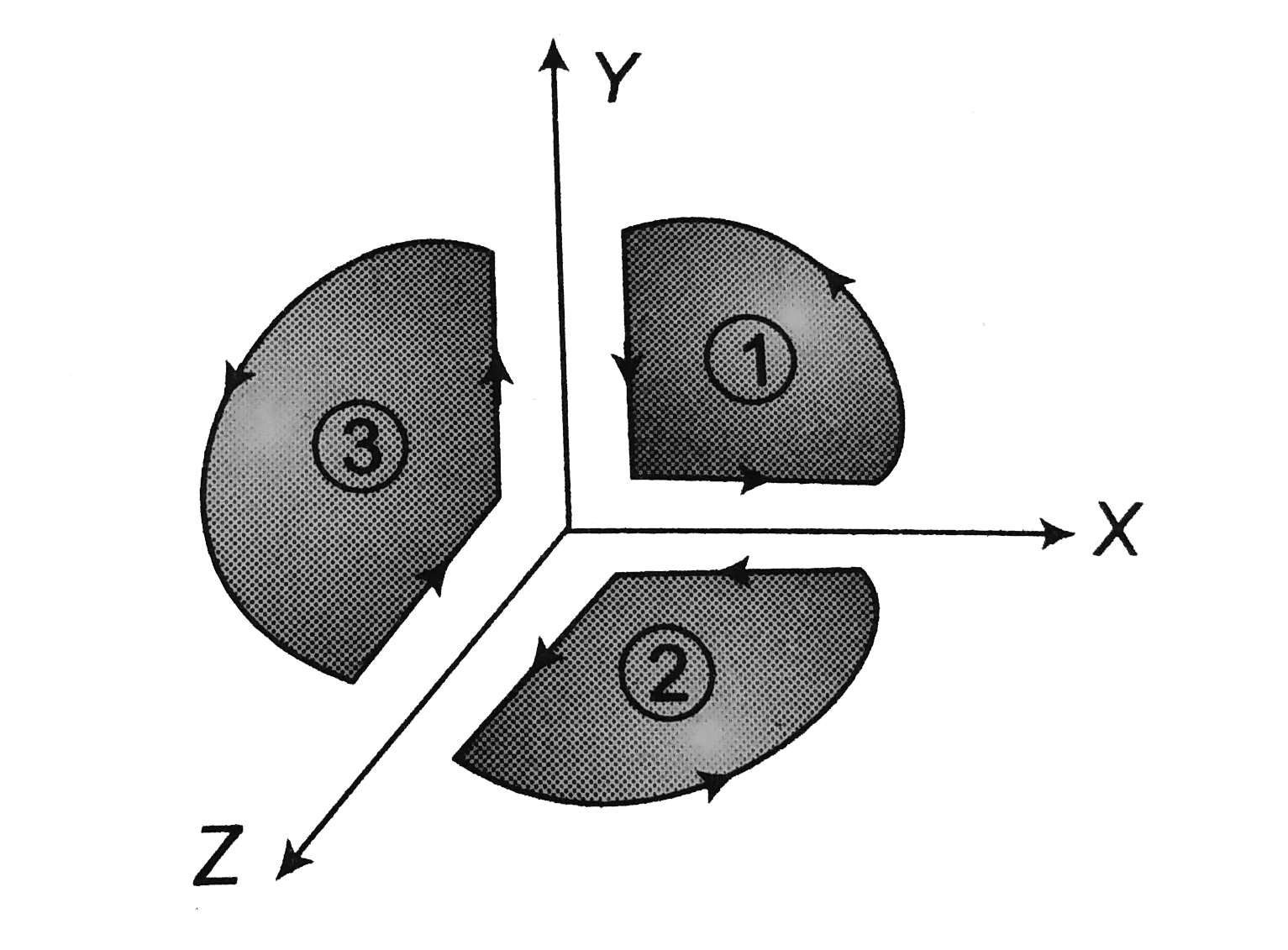
M1=i(πa24)ˆk
Similarly, M2=i(πa24)ˆj
M3=i(πa24)ˆi
So, net magnetic moment
→M=→M1+→M2+→M3
→M=πa2i4(ˆi+ˆj+ˆk)
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Current44videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Circular Arc69videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Force On A Current Carrying Conductor In Magnetic Field42videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE29videos
SEMICONDUCTOR ELECTRONICS
- BOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test29videos
WAVE OPTICS
Similar Questions
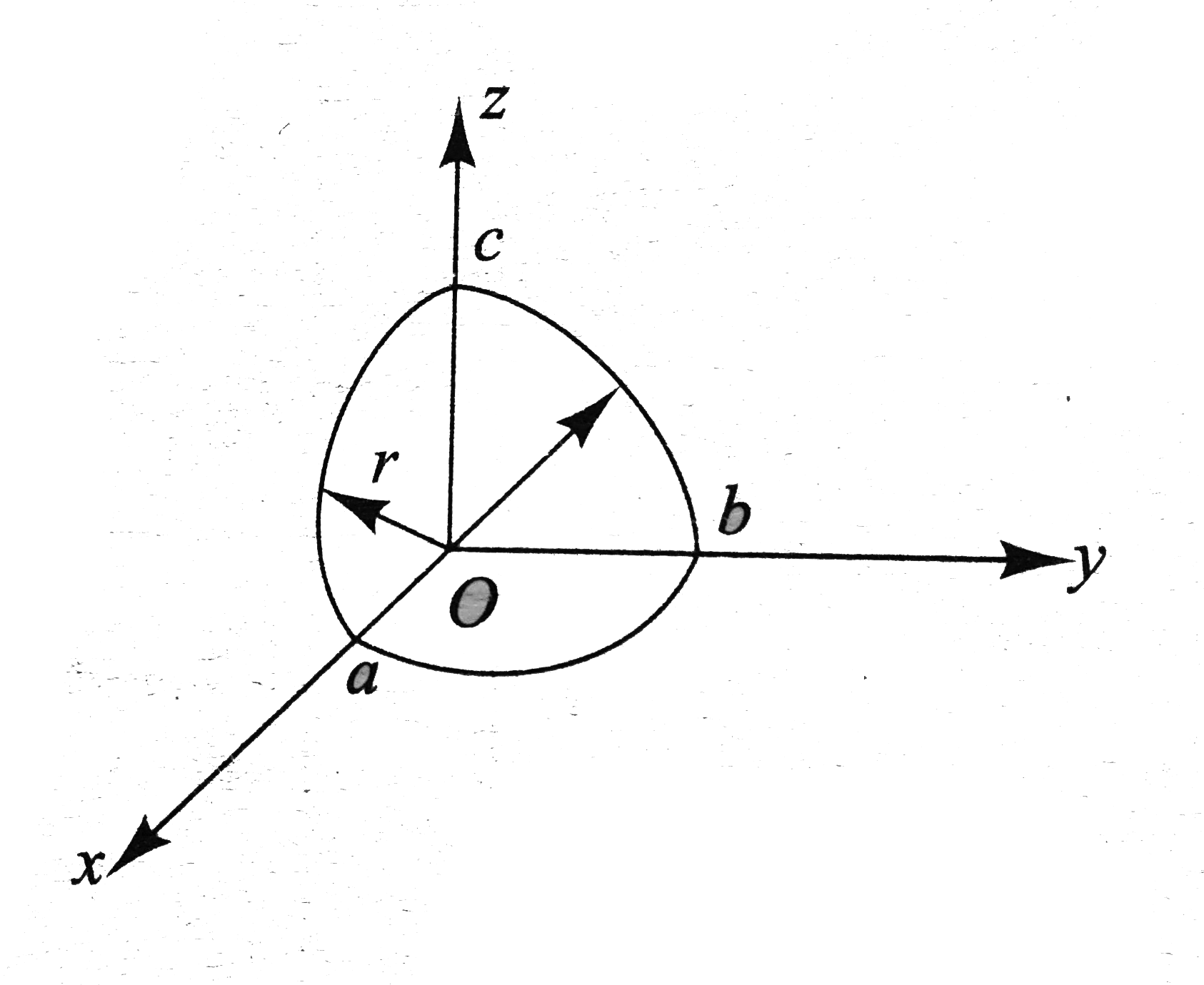
A wire is bent into three circular segment og radius r=10cm as shown in. Each segment is a quardrant of a circle ab lyinf in rthe x−y plane, bc lying in the y−z plane and ca lying in the z−x plane.
(a) if a magnetic field B points in the positive x direction, what is the magnitude of the emf developed in the wire when B increases at the rate of 3mTs−1?
(b) What is the direction of teh current in the segment bc.
 View Solution
View SolutionThree identical wires are bent into semi-circular arcs to each of radius R. These arcs are connected with each other to form a closed mesh such that one of tham lies in x−y plane, one in y−z plane and the other in z−x plane as shown in. In the region of space, a uniform magnetic field of induction →B=B0(ˆi+ˆj) exists, whose magnitude increases at a constant rate dB/dt=α. Calculate the magnitude of emf induced in the mesh and mark the direction of flow of induced current in the mesh.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A current carrying wire frame is in the shape of digit eight (8). It is carrying current i0. If the radius of each loop is R0, then the net magnetic dipole moment of the figure is :
 A(i0πR20)√2BzeroCi0×2πR20Di0×(4πR0)
A(i0πR20)√2BzeroCi0×2πR20Di0×(4πR0) - Question 2 - Select One
A current of 10 A is flowing through a circular coil of 5 turns each of radius 7 cm the coil lies in the X-Y plane what is the magnitude and direction of the magnetic dipole mometn associated with it ?
A0.47 am2 along Z axisB0.77Am2 along Z axisC0.77Am2 along Y axisD1.54Am2 - Question 3 - Select One
A wire of length l, carrying current i, is bent in circle of radius r, then magnetic momennt at centre of loop is
Al2i2πBl2i4πCli22πDli4π
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.
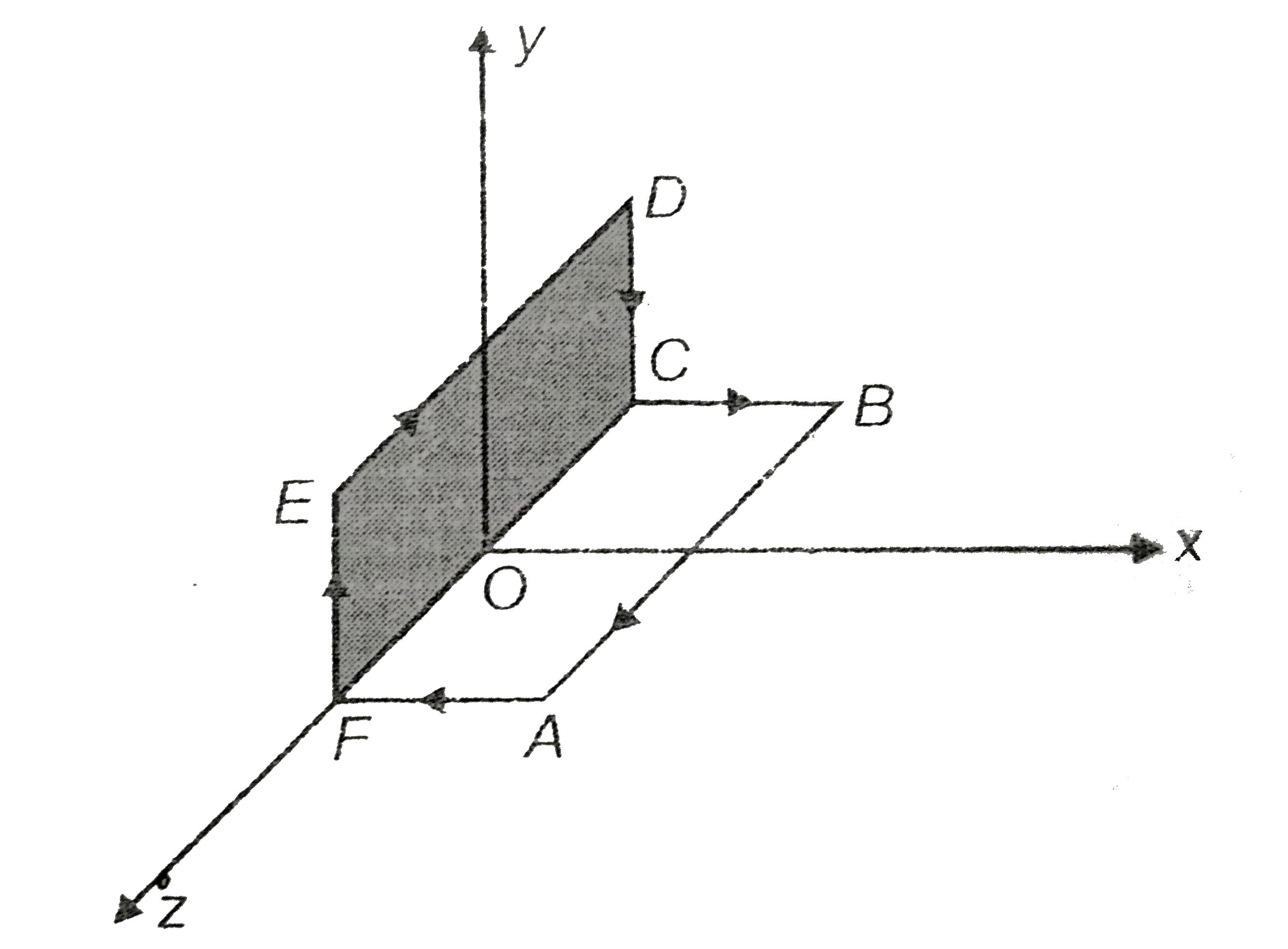
View SolutionCurrent is flowing in a wire frame kept as shown in the figure where EDCF is in y-z plane and AFCB is in x-z plane. Current in the wire frame is i and length of each side is a. Find the magnetic moment
 View Solution
View SolutionA conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is →B−8ˆk and the current in the wire is 2A.
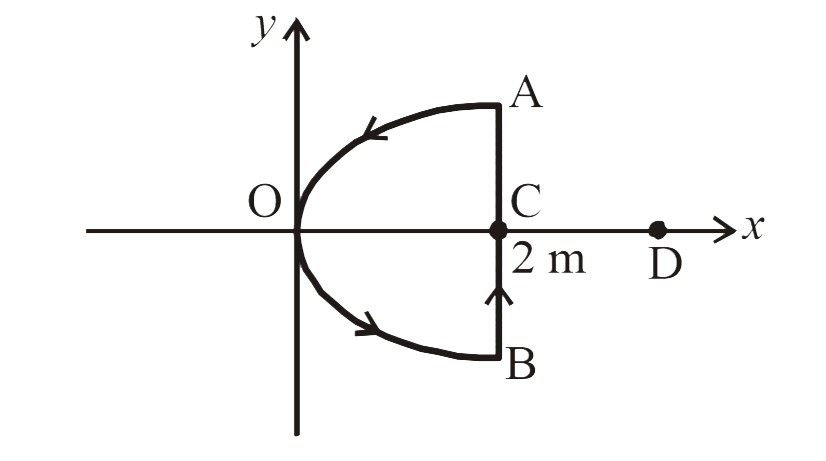
The torque on the loop will beView SolutionA conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is →B−8ˆk and the current in the wire is 2A.
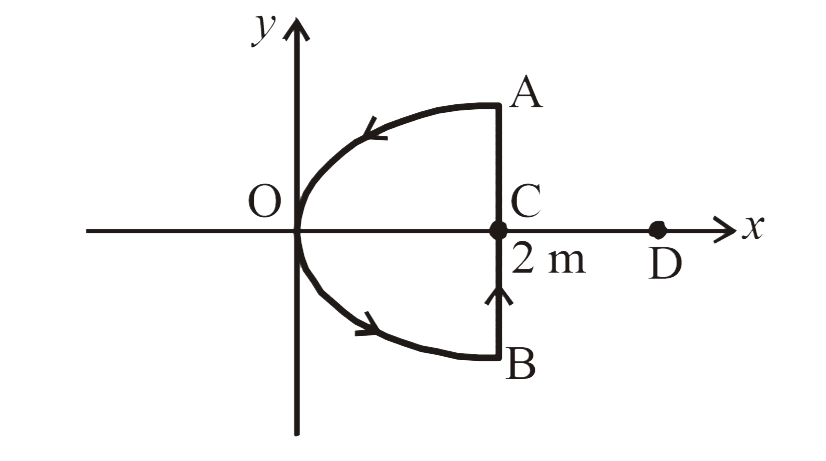
The field created by the current in the loop at point C will beView SolutionA wire loop consists of a straight segment AB and a circular are ACB of radius r The segment AB subtends an angle of 60∘ at the centre O of the circular are The wire loop carries a current I in the clockwise direction

The magnetic field B2 at O to the circular are ACB is .View Solution

