A wire of cross-sectional area A forms three sides of a square and is free to rotate about axis OO'. If the structure is deflected by an angle θ from the vertical when current i is passed through it in a magnetic field B acting vertically upward and density of the wire is ρ, then the value of θ is given by

2AρgiB=cotθ
2AρgiB=tanθ
AρgiB=sinθ
Aρg2iB=cosθ
The correct Answer is:a
Let a is the side of squre.

Torque of current =MBsin(90−θ)
=MBcosθ=ia2Bcosθ
Mass of each side =m=ρAa
Torque of gravity =2mga2sinθ+mgasinθ
=2mgasinθ=2ρAga2sinθ
Now, both torques should be same
i.e., ia2Bcosθ=2ρAga2sinθ
⇒cotθ=2ρAgiB
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Multiple Correct
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Subjective
10 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A wire bent in the form of a sector of radius r subtending an angle θ∘ at centre as shown in figure is carrying a current I. The magnetic field at O is :
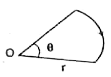
View SolutionWhen current is passed through a circular wire prepared from a conducting material, the magnetic field produced at its centre is B. Now a loop having two turns is prepared from the same wire and the same current is passed through it. The magnetic field at its centre will be :
View SolutionA wire of length l is formed into a circular loop of one turn only and is suspended in a magnetic field B. When a current i is passed through the loop, the maximum torque experienced by it is
View SolutionA stationary horizontal disc is free to rotate about its axis. When a torque is applied on it its, kinetic energy as a function of θ, where θ is the angle by which it has rotated, is given as kθ. If its moment of inertia is I then the angular acceleration of the disc is :
View SolutionA moving coil galvanometer coil has a coil of area A, number of turns N. The radial magnetic field present is B. the moment of inertia of the coil is I about its rotation axis. The torque is applied by the magnetic field on the coil of the galvanometer when current I0 passes through it and produces a deflection of π/2 of the pointer. Then answer the following questions based on the paragraph.
Then the value of torsionl constant of the spring is
View SolutionA circular coil of radius 20cm and 20 turns of wire is mounted vertically with its plane in magnetic meridian.A small magnetic needle (free to rotate about vertical axis) is placed at the center of the coil.It is deflected through 45∘ when a current is passed through the coil and in equilbrium (Horizontal component of earth's field is 0.34×10−4T).The current in coil is:
View SolutionA straight peice of conducting wire with mass M and length L is placed on a frictionless incline tilited at an angle θ from the horizontal (as shown in fig) There is a uniform. Vertical magnetic field at all points (produced by an arrangement of magnets not shown in fig. To keep the wire from sliding down the incline, a voltage source is

attached to the ends of the wire. When just the right amount of current flows through the wire, the wire remains at rest. Determine the magnitude and direction of the current in the wire that will cause the wire to remain at rest.
View SolutionA wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
View SolutionThe specific resistance and area of cross section of the potentiometer wire are ρ' and A respectively. If a current i passes through the wire, its potential gradient will be
View SolutionA current - carrying wire of certain length is bent to form an arc that substends an angle θ at the centre. Let B be the magnetic field at the centre due to this wire. The correct graph between B and θ is
View Solution
