Question

A current - carrying wire of certain length is bent to form an arc that substends an angle $\theta$ at the centre. Let B be the magnetic field at the centre due to this wire. The correct graph between B and $\theta$ is

Options

A.
B.
C.
D.

Answer

B

Explanation

To solve the problem, we need to determine the relationship between the magnetic field $$B$$ at the center of an arc of a current-carrying wire and the angle $$\theta$$ that the arc subtends at the center.

1. Understanding the Arc Length:
The length \( L \) of the arc is given by the formula:
\( L = r \cdot \theta \)
where \( r \) is the radius of the arc and \( \theta \) is in radians.

2. Expressing the Radius in Terms of Length and Angle:
Rearranging the above equation gives:
\( r = \frac{L}{\theta} \)

3. Magnetic Field Due to the Arc:
The magnetic field \( B \) at the center of the arc due to a current \( I \) flowing through it is given by:
\( B = \frac{\mu_0 I}{2r} \cdot \frac{\theta}{2\pi} \)
where \( \mu_0 \) is the permeability of free space.

4. Substituting for Radius:
Substitute \( r = \frac{L}{\theta} \) into the equation for \( B \):
\( B = \frac{\mu_0 I}{2 \cdot \frac{L}{\theta}} \cdot \frac{\theta}{2\pi} \)
Simplifying this gives:
\( B = \frac{\mu_0 I \cdot \theta}{4\pi L} \)

5. Identifying the Relationship:
From the equation \( B = k \cdot \theta \) where \( k = \frac{\mu_0 I}{4\pi L} \), we can see that \( B \) is directly proportional to \( \theta \).

6. Considering the Range of \( \theta \):
As \( \theta \) increases, \( B \) also increases linearly. However, if we consider the case where \( \theta \) approaches zero, \( B \) will also approach zero.

7. Graphing the Relationship:
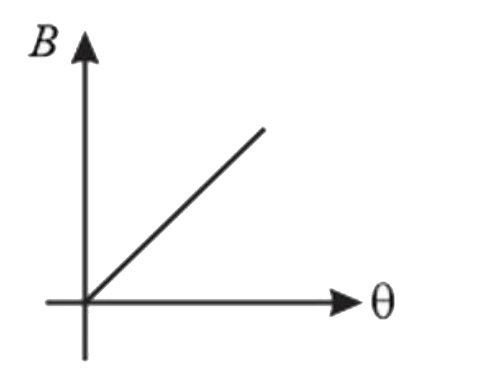
The graph of \( B \) versus \( \theta \) will be a straight line passing through the origin (0,0) and will have a positive slope.

Conclusion:
The correct graph between \( B \) and \( \theta \) is a straight line that passes through the origin.