A wire of length l and mass m is bent in the form of a rectangle ABCD with ABBC=2. The moment of inertia of this wife frame about the side BC is
22252ml2
8203ml2
5136ml2
7162ml2
The correct Answer is:D
To find the moment of inertia of the wire frame bent in the form of a rectangle ABCD about the side BC, we can follow these steps:
Step 1: Define the dimensions of the rectangle
Given that the ratio of the lengths of sides AB and BC is 2:1, we can let:
- AB=2x
- BC=x
Step 2: Calculate the perimeter and relate it to the length of the wire
The perimeter P of the rectangle is given by:
P=2(AB+BC)=2(2x+x)=6x
Since the total length of the wire is l, we have:
6x=l⟹x=l6
Step 3: Determine the lengths of the sides
Now substituting x back, we find:
- AB=2x=2⋅l6=l3
- BC=x=l6
Step 4: Calculate the mass distribution
The mass m of the wire is uniformly distributed along its length. The mass per unit length μ is:
μ=ml
Now, we can find the mass of each side:
- Mass of side AB (length l3):
mAB=μ⋅l3=ml⋅l3=m3
- Mass of side BC (length l6):
mBC=μ⋅l6=ml⋅l6=m6
- Mass of side CD is the same as AB:
mCD=mAB=m3
Step 5: Calculate the moment of inertia about side BC
The moment of inertia I about an axis through one end of a rod is given by:
I=13mL2
1. For sides AB and CD (both have length l3):
- Distance from BC to AB and CD is l6:
IAB=13(m3)(l3)2=13⋅m3⋅l29=ml281
Since ICD=IAB:
ICD=ml281
2. For side AD (length l6):
- The moment of inertia about BC is:
IAD=mAD⋅d2=(m6)(l3)2=m6⋅l29=ml254
Step 6: Sum the moments of inertia
The total moment of inertia Itotal about side BC is:
Itotal=IAB+ICD+IAD=2⋅ml281+ml254
Finding a common denominator (which is 162):
Itotal=2ml281+3ml2162=4ml2162+3ml2162=7ml2162
Final Result
Thus, the moment of inertia of the wire frame about the side BC is:
7ml2162
Given that the ratio of the lengths of sides AB and BC is 2:1, we can let:
- AB=2x
- BC=x
The perimeter P of the rectangle is given by:
P=2(AB+BC)=2(2x+x)=6x
Since the total length of the wire is l, we have:
6x=l⟹x=l6
Now substituting x back, we find:
- AB=2x=2⋅l6=l3
- BC=x=l6
The mass m of the wire is uniformly distributed along its length. The mass per unit length μ is:
μ=ml
Now, we can find the mass of each side:
- Mass of side AB (length l3):
mAB=μ⋅l3=ml⋅l3=m3
- Mass of side BC (length l6):
mBC=μ⋅l6=ml⋅l6=m6
- Mass of side CD is the same as AB:
mCD=mAB=m3
The moment of inertia I about an axis through one end of a rod is given by:
I=13mL2
1. For sides AB and CD (both have length l3):
- Distance from BC to AB and CD is l6:
IAB=13(m3)(l3)2=13⋅m3⋅l29=ml281
Since ICD=IAB:
ICD=ml281
- The moment of inertia about BC is:
IAD=mAD⋅d2=(m6)(l3)2=m6⋅l29=ml254
The total moment of inertia Itotal about side BC is:
Itotal=IAB+ICD+IAD=2⋅ml281+ml254
Finding a common denominator (which is 162):
Itotal=2ml281+3ml2162=4ml2162+3ml2162=7ml2162
Thus, the moment of inertia of the wire frame about the side BC is:
7ml2162
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE41videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - COMPREHENSION_TYPE29videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN12videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem4videos
UNIT AND DIMENSIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In a rectangle ABCD (BC=2AB). The moment of inertia along which axis will be minimum
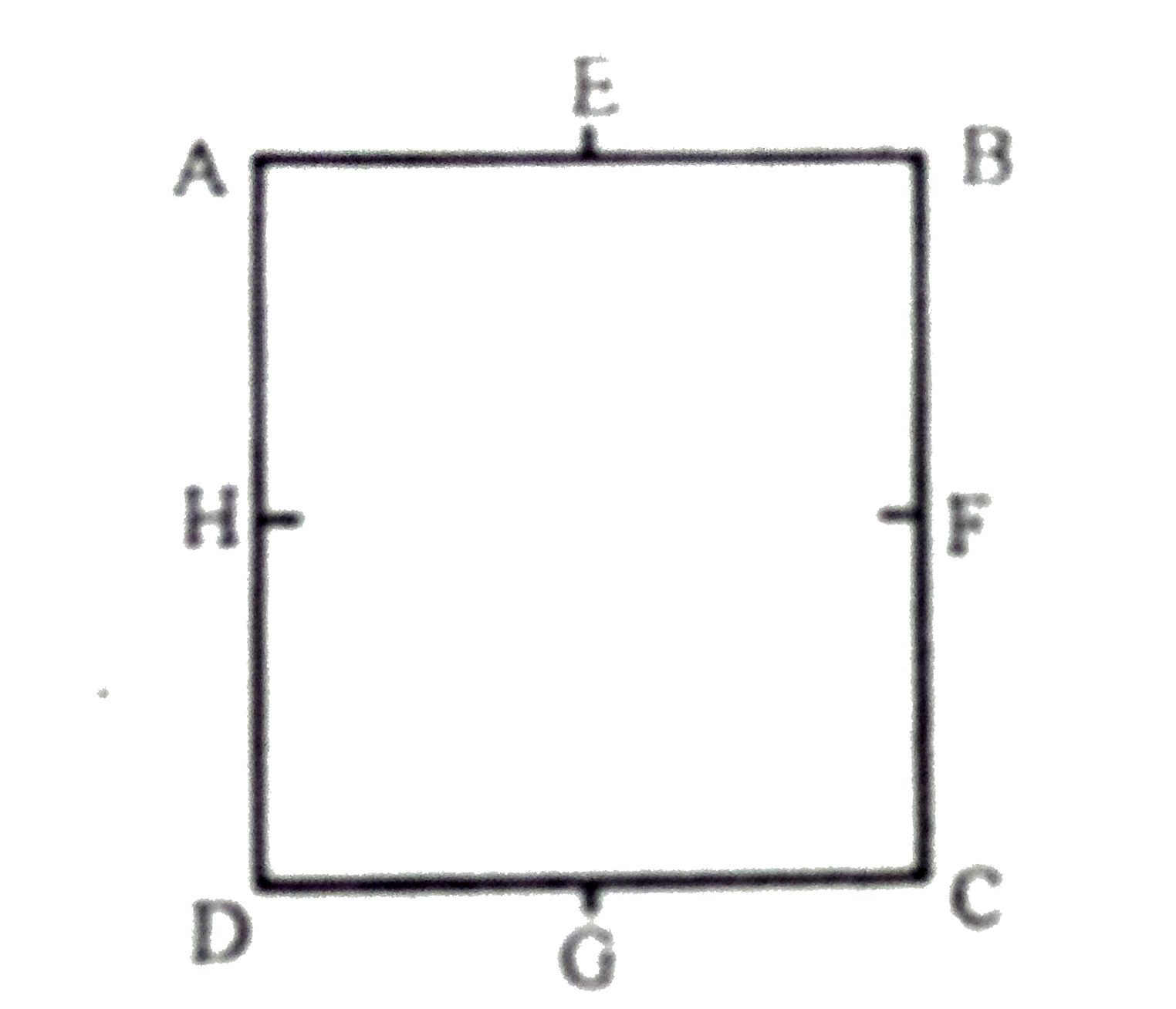 AEGBHFCBDDBC
AEGBHFCBDDBC - Question 2 - Select One
In a rectangle ABCD (BC=2AB). The moment of inertia along which the axis will be minimum
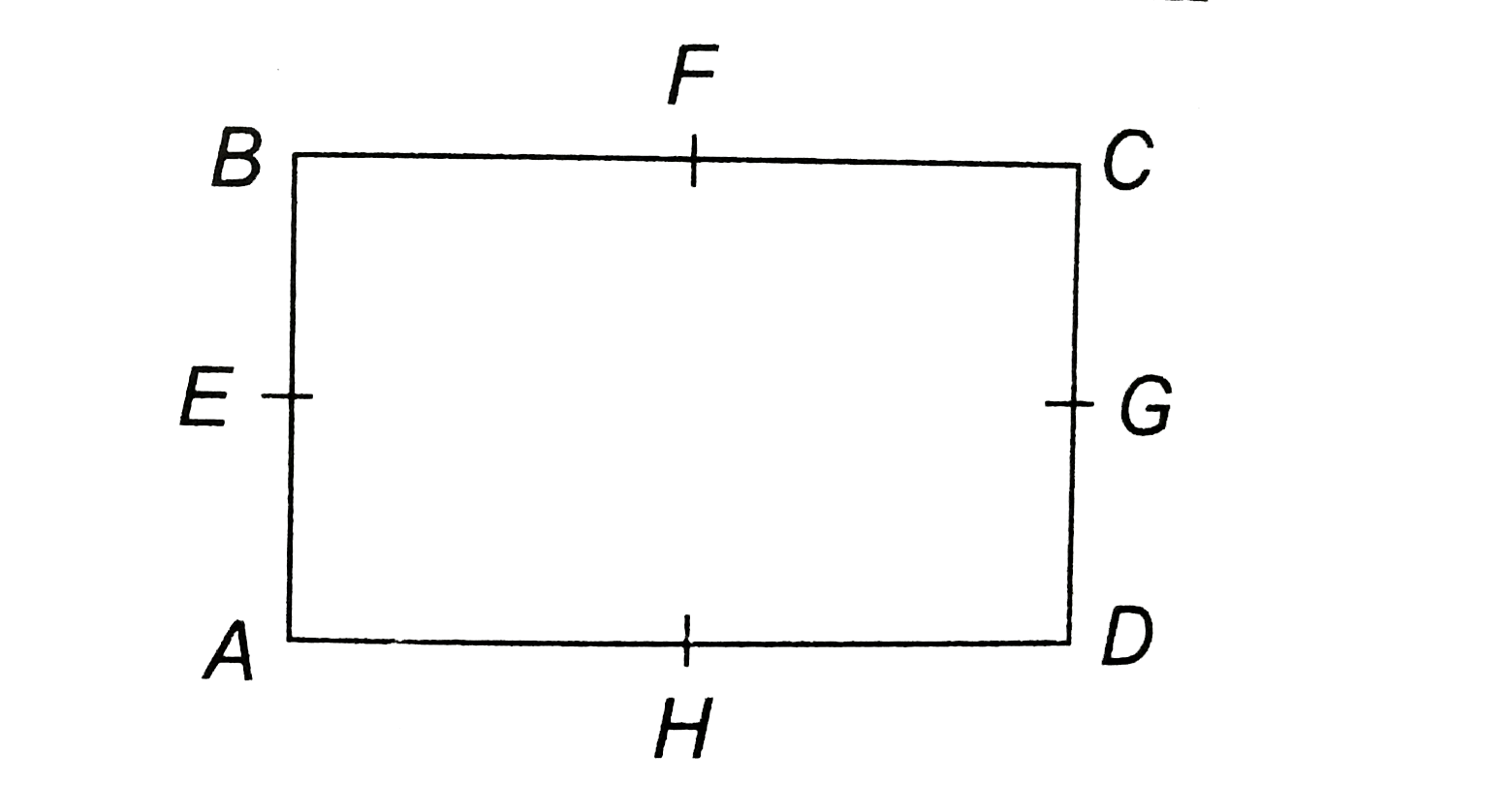 ABCBBDCHFDEG
ABCBBDCHFDEG - Question 3 - Select One
In a rectangle ABCD(BC=2AB). The moment of inertia is minimum along axis through
 ABCBBDCHFDEG
ABCBBDCHFDEG
A thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
 View Solution
View SolutionA thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
 View Solution
View SolutionA wire of mass 'm' and length 'l' is bent in the form of a circular ring. The moment of inertia of the ring about its axis is-
View SolutionA thin wire of length l and mass m is turned into the form of a semicircle. Its moment of inertia about an axis joining its free ends will be
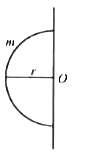 View Solution
View SolutionA wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
View Solution


