A wire of length L is hanging from a fixed support. The length changes to L1andL2 when masses M1andM2 are suspended respectively from its free end. Then L is equal to
L1+L22
√L1L2
L1M2+L2M1M1+M2
L1M2−L2M1M2−M1
The correct Answer is:D
Let L be the original length of the wire

When the mass M1 is suspended from the wire, change in length of wire is ΔL1=L1−L
When the mass M2 is suspended from it, change in length of wire is
ΔL2=L2−L
From figure (b), T1=M1g ...(i)
From figure (c ), T2=M2g ...(ii)
As Young.s modulus, Y=T1LAΔL1=T2LAΔL2
∴T1ΔL1=T2ΔL2orT1L1−L=T2L2−L
or M1gL1−L=M2gL2−L (Using (i) and (ii))
or M1(L2−L)=M2(L1−L)orM1L2−M1L=M2L1−M2L
or L(M2−M1)=L1M2−L2M1
or L=L1M2−L2M1M2−M1
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Check Your Neet Vitals
22 Videos
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)
40 Videos
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)
40 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ
14 Videos
- THERMODYNAMICSBOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)
26 Videos
Similar Questions
A wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionThe value of tension in a long thin metal wire has been changed from T1 to T2. The lengths of the metal wire at two different values of tension T1 and T2 are l1andl2 respectively. The actual length of the metal wire is :
View Solution
Knowledge Check
A wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
AMg(L1−L)ALBMgLAL1CMgLA(L1−L)DMgL1ALThe balancing lengths for the cells of e.m.f. E1 and E2 are l1 and l2 respectively. If they are connected separately then
AE1E2=l1l2BE1E2=l1+l2l1−l2CE1E2=l1+l2l2DE1E2=l1−l2l2A string of length L and mass M hangs freely from a fixed point. Then the velocity of transverse waves along the string at a distance x from the free end is
A√gLB√gxCgLDgx
The length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
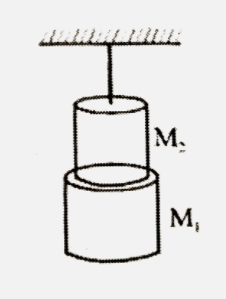
View SolutionTwo point masses m1 and m2 are fixed to a light rod hinged at one end. The masses are at distances l1 and l2 repsectively from the hinge. Find the time period of oscillation (small amplitude) of this system in seconds if m1=m2,l1=1m,l2=3m. If the time period is xπ, then find x.

View SolutionWhen a thin iron wire of length l is heated from a temperature T1 to T2 , a change of 1% in its length is observed. The percentage change in area of iron plate of dimension 2l×l when it is heated from T1 to T2 is
View SolutionTwo wires of equal diameters, of resistivities ρ1 and ρ2 and length l1 and l2, respectively of the combination is
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View Solution
