The value of tension in a long thin metal wire has been changed from T1 to T2. The lengths of the metal wire at two different values of tension T1 and T2 are l1andl2 respectively. The actual length of the metal wire is :
T1l2−T2l1T1−T2
T1l1−T2l2T1−T2
l1+l22
√T1T2l1l2
To find the actual length of the metal wire, we can use the relationship between tension, stress, strain, and the lengths of the wire under different tensions. Let's denote the actual length of the wire as L0.
1. Understanding the Problem:
We have a metal wire that experiences two different tensions T1 and T2, resulting in lengths L1 and L2 respectively. We need to find the actual length L0 of the wire.
2. Using the Relationship of Stress and Strain:
The stress in the wire can be defined as:
Stress=TA
where T is the tension and A is the cross-sectional area of the wire.
The strain can be defined as:
Strain=ΔLL0=L−L0L0
where L is the length of the wire under tension and ΔL is the change in length.
3. Applying Hooke's Law:
According to Hooke's law, we have:
Stress=Y⋅Strain
where Y is the Young's modulus of the material.
4. Setting Up the Equations:
For the first case with tension T1:
T1A=Y⋅L1−L0L0
Rearranging gives:
T1=Y⋅(L1−L0)L0⋅A(Equation 1)
For the second case with tension T2:
T2A=Y⋅L2−L0L0
Rearranging gives:
T2=Y⋅(L2−L0)L0⋅A(Equation 2)
5. Dividing the Two Equations:
Dividing Equation 1 by Equation 2:
T1T2=L1−L0L2−L0
6. Cross Multiplying:
Rearranging gives:
T1(L2−L0)=T2(L1−L0)
7. Expanding and Rearranging:
Expanding both sides:
T1L2−T1L0=T2L1−T2L0
Rearranging to isolate L0:
T1L2−T2L1=L0(T1−T2)
8. Solving for L0:
Finally, we can solve for L0:
L0=T1L2−T2L1T1−T2
Final Answer:
The actual length of the metal wire is:
L0=T1L2−T2L1T1−T2
We have a metal wire that experiences two different tensions T1 and T2, resulting in lengths L1 and L2 respectively. We need to find the actual length L0 of the wire.
The stress in the wire can be defined as:
Stress=TA
where T is the tension and A is the cross-sectional area of the wire.
Strain=ΔLL0=L−L0L0
where L is the length of the wire under tension and ΔL is the change in length.
According to Hooke's law, we have:
Stress=Y⋅Strain
where Y is the Young's modulus of the material.
For the first case with tension T1:
T1A=Y⋅L1−L0L0
Rearranging gives:
T1=Y⋅(L1−L0)L0⋅A(Equation 1)
T2A=Y⋅L2−L0L0
Rearranging gives:
T2=Y⋅(L2−L0)L0⋅A(Equation 2)
Dividing Equation 1 by Equation 2:
T1T2=L1−L0L2−L0
Rearranging gives:
T1(L2−L0)=T2(L1−L0)
Expanding both sides:
T1L2−T1L0=T2L1−T2L0
Rearranging to isolate L0:
T1L2−T2L1=L0(T1−T2)
Finally, we can solve for L0:
L0=T1L2−T2L1T1−T2
The actual length of the metal wire is:
L0=T1L2−T2L1T1−T2
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION-B)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - A)
40 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
Knowledge Check
If 'O' is at equilibrium then the values of the tension T1 and T2 respectively.
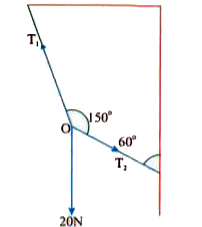 A20N, 30 NB20√3N,20NC20√3N,20√3ND10N, 30 N
A20N, 30 NB20√3N,20NC20√3N,20√3ND10N, 30 NThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
Al1+l22B√(l1l2)Cl1T2−l2T1T2−T1Dl1T2−l2T1T1+T2Two wires of equal diameters, of resistivities ρ1 and ρ2 and length l1 and l2, respectively of the combination is
Aρ1l1+ρ2l2l1+l2Bρ1l2+ρ2l1l1−l2Cρ1l2+ρ2l1l1+l2Dρ1l1+ρ2l2l1−l2
The length of a metal wire is l1 when the tensionin it is T1andisl2 when the tension is T2. The natural length of the wire is
View SolutionThe length of a steel wire is l1 when the stretching force is T1 and l2 when the stretching force is T2. The natural length of the wire is
View SolutionThe current (I) and voltage (V) graphs for a given metallic wire at two different temperature (T1) and (T2) are shown in fig. It is concluded that

View SolutionIf O is at equilibrium then the values of the tension T1 and T2 are, (20N is acting vertically downwards at O).
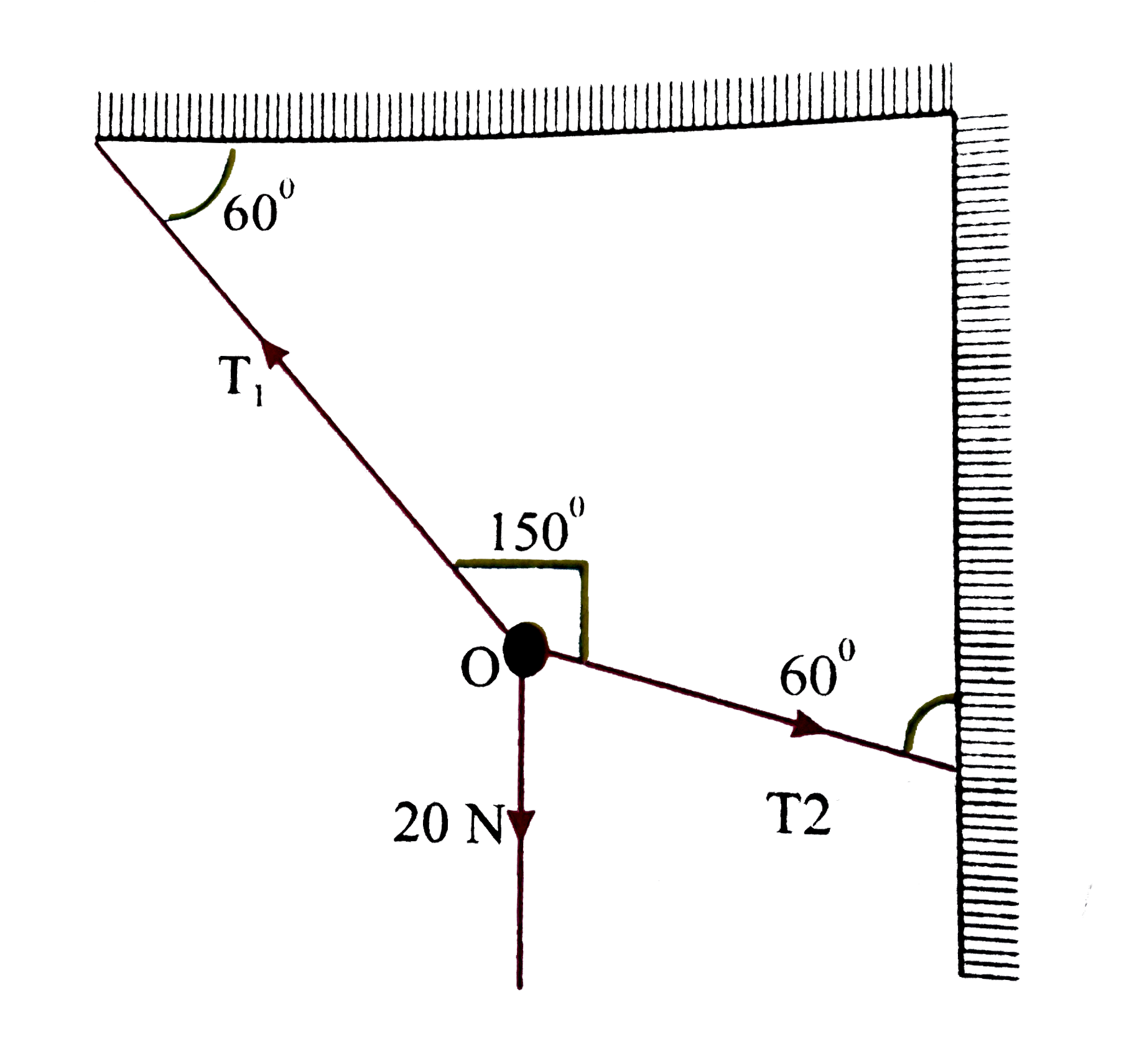
View SolutionThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
View Solution