A woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100N over a distance of 10m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50N. The total distance through which trunk has been moved is 20m. Plot the force applied by the woman and the frictional force, which is 50N against the distance. Calculat the work done by the two forces over 20m.
To solve the problem step by step, we will follow the instructions given in the question and calculate the work done by the woman and the frictional force.
Step 1: Understanding the Forces
- The woman applies a force of 100 N for the first 10 m.
- After 10 m, her force decreases linearly to 50 N by the time she has pushed the trunk for a total distance of 20 m.
- The frictional force opposing her push is constant at 50 N.
Step 2: Plotting the Forces
1. Force Applied by the Woman:
- From 0 to 10 m, the force is constant at 100 N.
- From 10 m to 20 m, the force decreases linearly from 100 N to 50 N.
- This can be represented as two segments on the graph:
- A horizontal line at 100 N from 0 to 10 m.
- A straight line decreasing from (10 m, 100 N) to (20 m, 50 N).
2. Frictional Force:
- The frictional force is constant at -50 N (negative because it opposes the motion).
- This can be represented as a horizontal line at -50 N from 0 to 20 m.
Step 3: Calculating the Work Done by the Woman
- Area under the Force vs. Distance graph:
- The work done by the woman can be calculated as the area under the force vs. distance graph.
1. Area of Rectangle (0 to 10 m):
- Length = 10 m
- Height = 100 N
- Area = Length × Height = 10 m × 100 N = 1000 J.
2. Area of Trapezium (10 to 20 m):
- The trapezium has bases of 100 N and 50 N, and a height of 10 m (from 10 m to 20 m).
- Area = (1/2) × (Base1 + Base2) × Height
- Area = (1/2) × (100 N + 50 N) × 10 m
- Area = (1/2) × 150 N × 10 m = 750 J.
3. Total Work Done by the Woman:
- Total Work = Work from Rectangle + Work from Trapezium
- Total Work = 1000 J + 750 J = 1750 J.
Step 4: Calculating the Work Done by the Frictional Force
- The work done by the frictional force is calculated as:
- Work = Force × Distance.
- Here, the frictional force is -50 N and the distance is 20 m.
- Work = -50 N × 20 m = -1000 J.
Summary of Results
- Work done by the woman = 1750 J.
- Work done by the frictional force = -1000 J.
- The woman applies a force of 100 N for the first 10 m.
- After 10 m, her force decreases linearly to 50 N by the time she has pushed the trunk for a total distance of 20 m.
- The frictional force opposing her push is constant at 50 N.
1. Force Applied by the Woman:
- From 0 to 10 m, the force is constant at 100 N.
- From 10 m to 20 m, the force decreases linearly from 100 N to 50 N.
- This can be represented as two segments on the graph:
- A horizontal line at 100 N from 0 to 10 m.
- A straight line decreasing from (10 m, 100 N) to (20 m, 50 N).
- The frictional force is constant at -50 N (negative because it opposes the motion).
- This can be represented as a horizontal line at -50 N from 0 to 20 m.
- Area under the Force vs. Distance graph:
- The work done by the woman can be calculated as the area under the force vs. distance graph.
1. Area of Rectangle (0 to 10 m):
- Length = 10 m
- Height = 100 N
- Area = Length × Height = 10 m × 100 N = 1000 J.
- The trapezium has bases of 100 N and 50 N, and a height of 10 m (from 10 m to 20 m).
- Area = (1/2) × (Base1 + Base2) × Height
- Area = (1/2) × (100 N + 50 N) × 10 m
- Area = (1/2) × 150 N × 10 m = 750 J.
- Total Work = Work from Rectangle + Work from Trapezium
- Total Work = 1000 J + 750 J = 1750 J.
- The work done by the frictional force is calculated as:
- Work = Force × Distance.
- Here, the frictional force is -50 N and the distance is 20 m.
- Work = -50 N × 20 m = -1000 J.
- Work done by the woman = 1750 J.
- Work done by the frictional force = -1000 J.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Conceptual Problems
27 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.
54 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Curiosity questions
2 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A gardener pushes a lawn roller on a rough surface. He applies a force of 150 N over a distance of 5 m. After he gets tired and his applied force reduces linerly with distance to 75 N. The total distance moved is 10 m. Plot the force applied by the gardencer and the frictional force, which is 75 N versus displacement. Calculate the work done by t he two forces over 10 m.
View SolutionA person pushes a box on a rough horizontal plateform surface.He applies a force of 200 N over a distance of 15 m. Therefore, he gets progressively tired and his applied force reduces linearly with distance to 100 N. The total distance through which the box has been moved is 30 m. What is the work done by the person during the total movement of the box?
View Solution
Knowledge Check
A force F is applied on a lawn move at an angle of 60∘ with the horizontal. If it moves through a distance x, the work done by the force is
AFx/2BF/2xC2FxD2x/FA constant force of 5 N is applied on a block of mass 20 kg for a distance 2 0 m. The kinetic energy acquired by the block is
A20 JB15 JC10 JD5 JA person is not able to push a box lying on the ground by applying a force. The force applied by the person is_____ static friction force.
Aless thanBgreater thanCequal toDnone of these
A woman pushes a trunk on a railway platform that has a rough surface, She applies a force F over a distance of 20 m as shown by the graph.
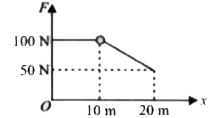
Calculate the work done by the woman.
View SolutionA body acted upon by a force of 50N is displaced through a distance of 10m in a direction making an angle of 60∘ with the force. Calculate the work done by the force.
View SolutionA force of 8 N is applied to a body at a distance of 20 cm from the point at which it is pivoted. Calculate the torque or moment of force about the pivot.
View SolutionHow much work is done by a force of 10 N in moving an object through a distance of 1 m in the direction of the force ?
View SolutionIf a person moves a trolley for a distance of 10 m with a force of 50 , then the work done is:
View Solution
