A wooden block is on the bottom of a tank when water is poured in. The contact between the block and the tank is so good that no water gets between them. Is there a buoyant force on the block?
To determine whether there is a buoyant force acting on the wooden block in the given scenario, we can follow these steps:
1. Understand the Concept of Buoyant Force:
- Buoyant force is the upward force exerted by a fluid on an object that is submerged in it. This force is equal to the weight of the fluid that the object displaces.
2. Analyze the Situation:
- The wooden block is resting on the bottom of the tank. When water is poured into the tank, the block remains in contact with the bottom and no water gets between the block and the tank.
3. Identify the Position of the Block:
- Since the block is on the bottom of the tank and there is no water underneath it, the block is not submerged in water.
4. Determine the Presence of Water Under the Block:
- For a buoyant force to act on the block, there must be water (or any fluid) underneath it to exert an upward force. In this case, there is no water beneath the block.
5. Conclusion:
- Since there is no water under the block, there is no upward force exerted on it. Therefore, the buoyant force acting on the block is zero.
Final Answer:
There is no buoyant force on the wooden block because there is no water underneath it to exert an upward force.
---
- Buoyant force is the upward force exerted by a fluid on an object that is submerged in it. This force is equal to the weight of the fluid that the object displaces.
- The wooden block is resting on the bottom of the tank. When water is poured into the tank, the block remains in contact with the bottom and no water gets between the block and the tank.
- Since the block is on the bottom of the tank and there is no water underneath it, the block is not submerged in water.
- For a buoyant force to act on the block, there must be water (or any fluid) underneath it to exert an upward force. In this case, there is no water beneath the block.
- Since there is no water under the block, there is no upward force exerted on it. Therefore, the buoyant force acting on the block is zero.
There is no buoyant force on the wooden block because there is no water underneath it to exert an upward force.
Topper's Solved these Questions
- Mechanical Properties of fluidsBOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise
459 Videos
- Mathematical toolsBOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise
20 Videos
- Mechanical Properties of SolidsBOOK - SL ARORACHAPTER - Mechanical Properties of SolidsEXERCISE - Example
113 Videos
Similar Questions
Knowledge Check
A wooden block is taken to the bottom of a lake of water and then released, it rise up with a
Aconstant accelerationBDecreasing accelerationCConstant velocityDDecreasing velocity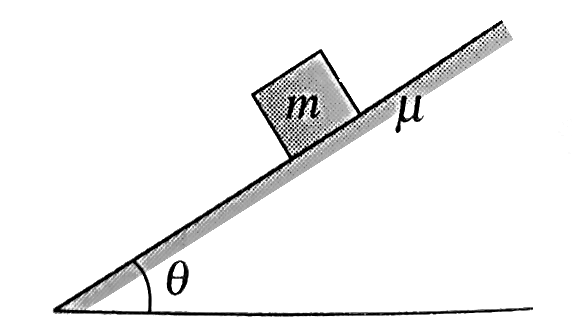
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If μ=34 then what will be frictional force (shear force) acting between the block and inclined plane when θ=30∘:A3√38mgBmg2C√32mgDzeroA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
AmgBmgsinθ√1+μ2CmgsinθD√(mgsinθ)2+(μmgcosθ)2
A block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View Solution
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. For what value of θ will the block slide on the inclined plane:
View SolutionA block of mass m is placed on a rough inclined plane. The coefficient of friction between the block and the plane is μ and the inclination of the plane is θ. Initially theat−0 and the block will certain stationary on the plane. Now the inclination θ is gradually increased. The block presses the inclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the block starts sliding, the angle θ for which the block starts sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction ( frictional force) and the shear reaction (frictional force) . The net contact force will be resultant of both.
If the entire system, were accelerated upward with acceleration 'a', the angle of repose , would :
View Solution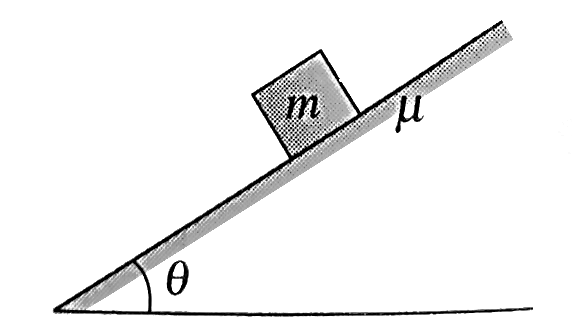
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If the entire system, were accelerated upward with acceleration a the angle of repose, would:
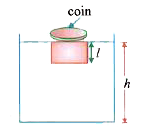
View SolutionA wooden block with a coin placed on its top floats in water as shown. After some time the coin falls into water.Then
View Solution