A wooden block of cross-sectional area 10cm2 is floating vertically on water. The volume of the immersed portion of the block is 200cm3. The block is depressed slightly inside water and then released. Calculate the time period of vibration of the block.
Volume of displaced water = 200cm3
∴ Mass of displaced water = 200 g, and mass of the wooden block = 200 g
Let the block be depressed inside water through x cm and then released.
∴ Upward restoring force on the block,
F=10x×1×g=10xg
∴ Acceleration of the block,
a=Fm=10xg200=xg20
∴ Time period of vibration of the block,
T=2π√xa=2π√20g=2π√20980=0.897s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SECTION RELATED QUESTIONS
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
32 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - CBSE SCANNER
10 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - CBSE SCANNER
3 Videos
Similar Questions
A cylindrical of wood (density =600kgm−3) of base area 30cm2 and height 54cm, floats in a liquid of density 900kg−3 The block is deapressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly) :
View SolutionA wooden block of mass 20 gram and cross section 20 cm2 is floating on the surface of water. If it is slightly depressed and released from the equilibrium position, then calculate the frequency of oscillation of the block if specific gravity of wood is 0.28.
View Solution
Knowledge Check
A cylindrical of wood (density =600kgm−3) of base area 30cm2 and height 54cm, floats in a liquid of density 900kg−3 The block is deapressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly) :
A26cmB52cmC36cmD65cmA uniform solid bar of wood floats vertically in water with 10 cm of its height immersed in the water. When it is slightly depressed and released, it oscillates with a frequency of
Aπ7HzB√2π7HzC7πHzD7√2πHzThe R.D of a metal block is 2.7×103kg/m3. It is immersed in water. Then the block
AsinksBflotsCis partially immersedDhas no part immersed
A block of wood of volume 30cm3 floats in water with 20cm3 of its volume immersed.
Calculate the weight of the block of wood .
View SolutionA cylinderical wooden block of cross-section 15.0 cm2 and mass 230g is floated over water with an extra weight of 50 g attached to its bottom. The cylider floats vertically. From the state of equilibrium, it is slightly depressed and released. If the specific gravity of wood is 0.30 and g=9.8ms−2 deduce the frequency of the block, A=15.0cm2=15×10−4m2
View SolutionA cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
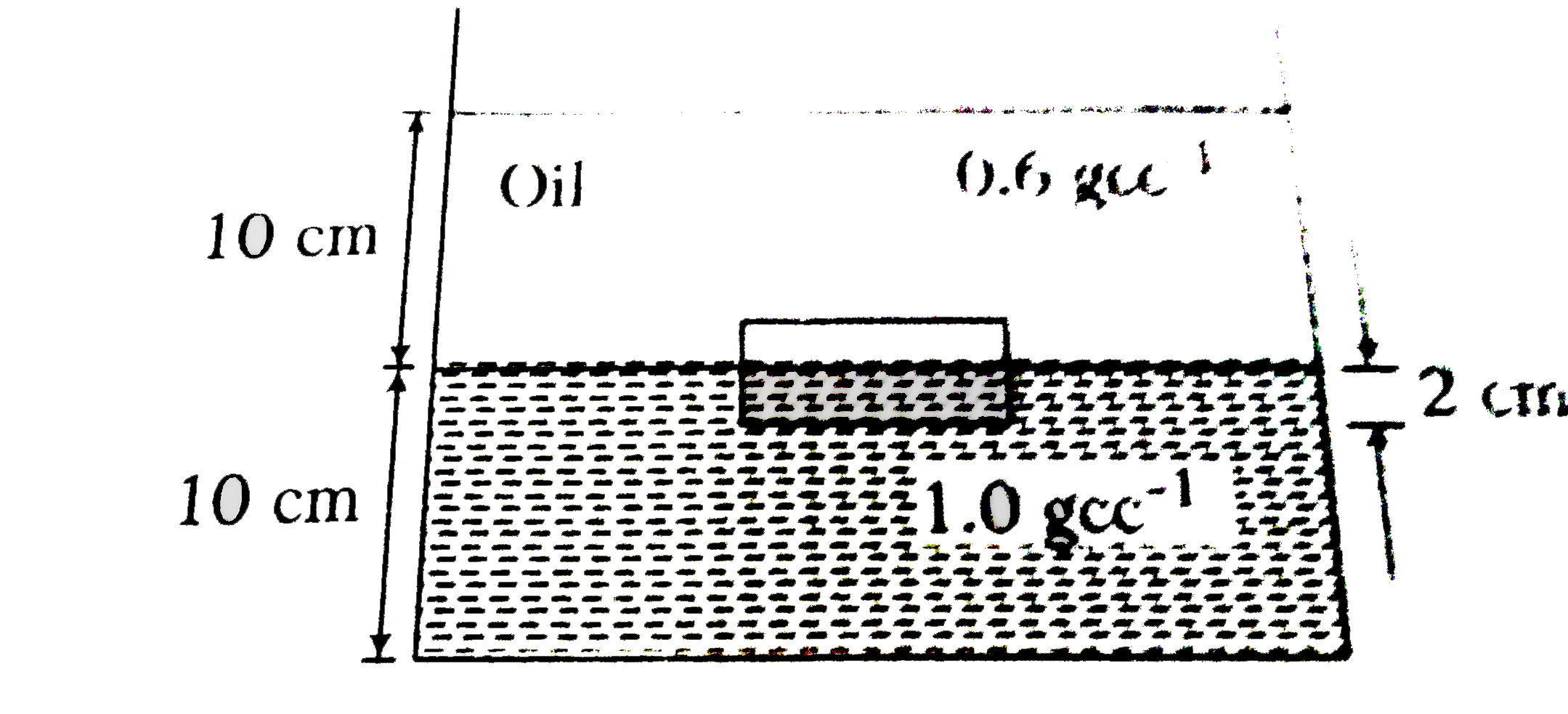
View SolutionA wooden block is taken to the bottom of a lake of water and then released, it rise up with a
View SolutionA cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
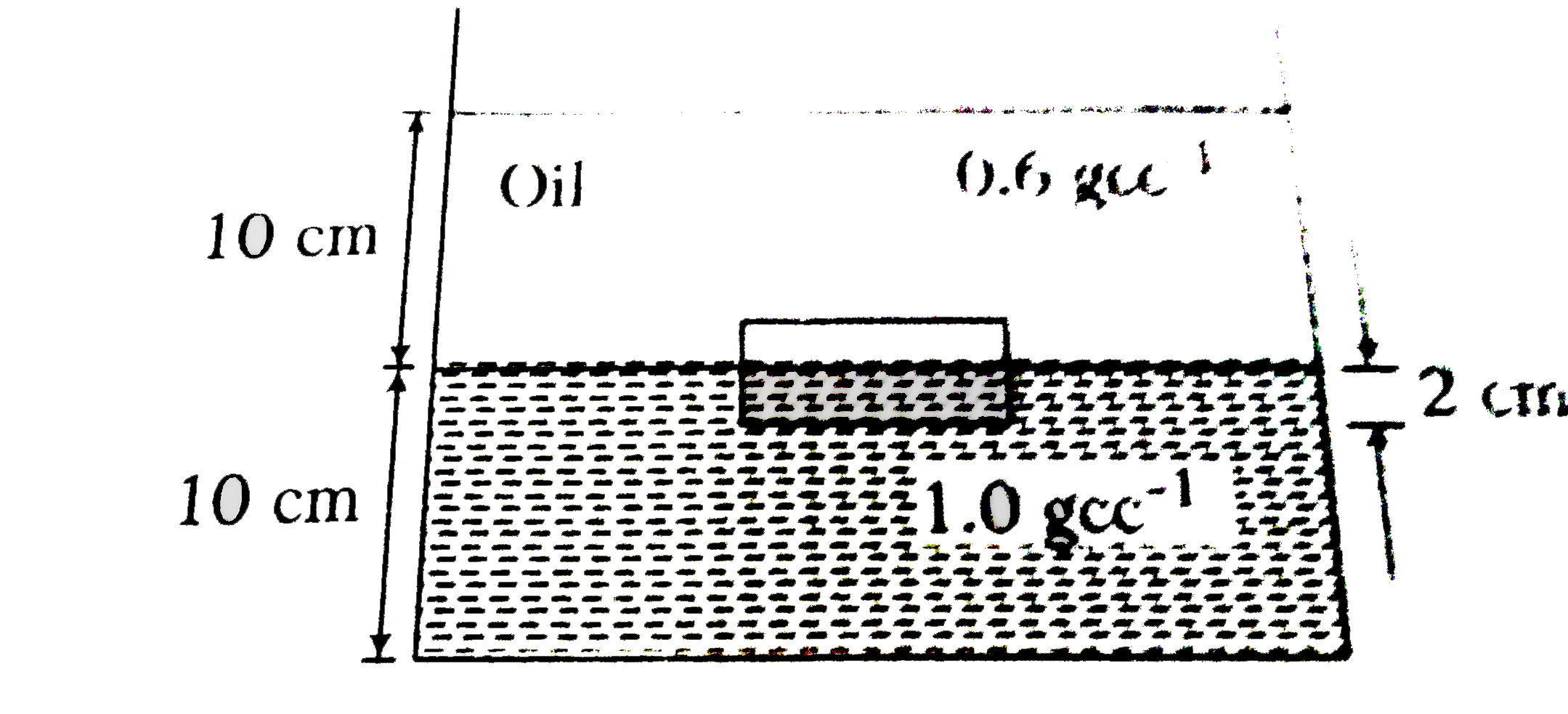
View Solution
