A wooden log of mass M and length L is hinged by a frictionless nail at O. A bullet of mass m strikes with velocity v and sticks to it. Find the angular velocity of the system, immediately after the collision about O. Also, calculate the minimum value of v so that log becomes horizontal after collision.
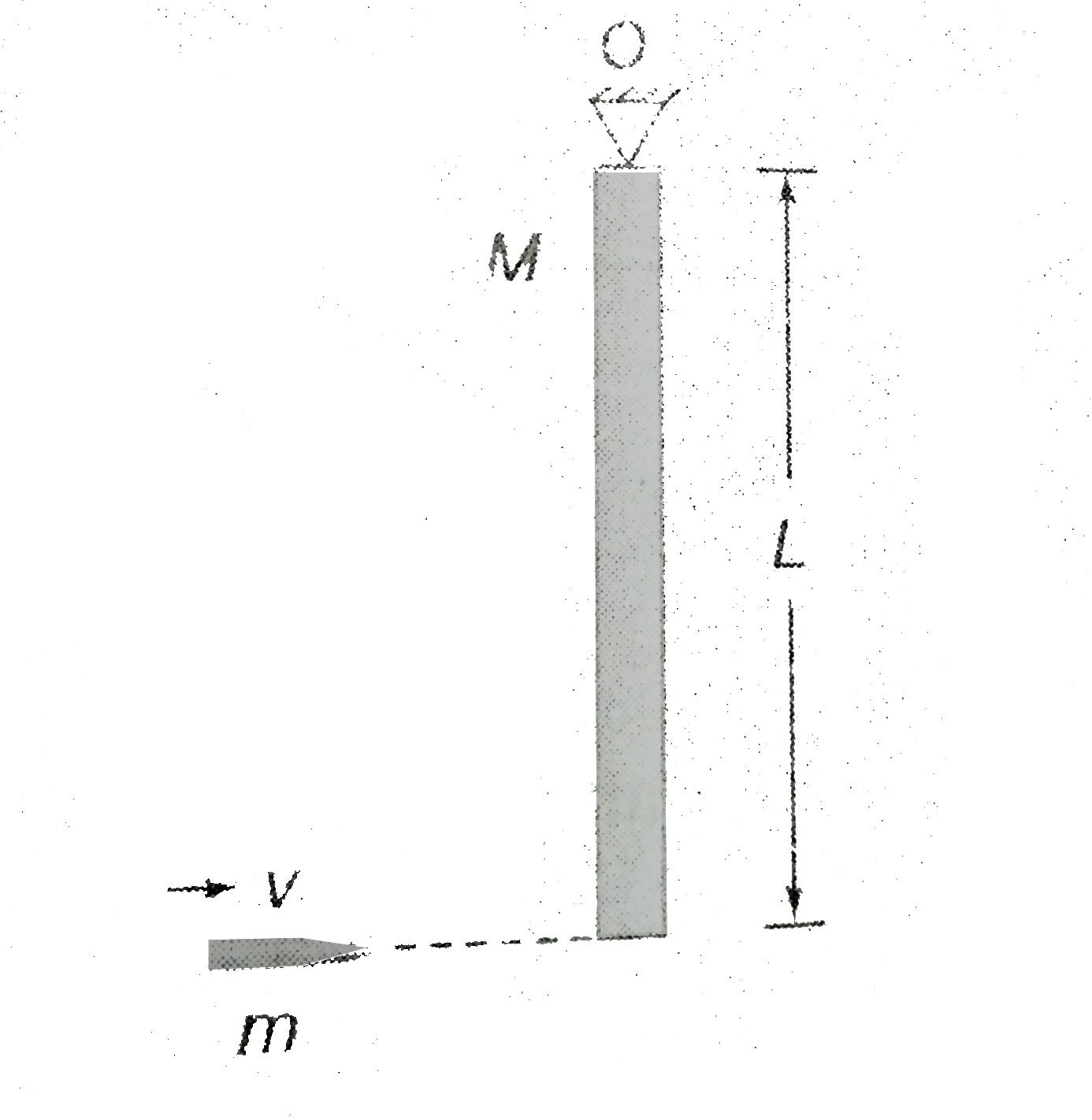

By the conservation of angular momentum about O between (1) and (2)
mvL=I0ω=(mL2+ML23)ω
ω=3mv(M+3m)L
Takin O as reference level, applying energy conservation between (2) and (3)
−mgl−Mg(L2)+12I0ω2=0
(M+2m)gL2=12(M+3m)L23×[3mv(M+3m)L]2
(M+2m)gL=3m2v2(M+3m)
v=(M+3m)(M+2m)gL3m2=vmin
Topper's Solved these Questions
Similar Questions
A wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.
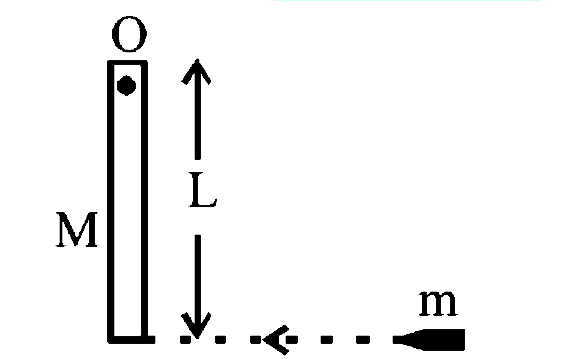 View Solution
View SolutionA wodden log mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and strikes with velocity v and sticks to it . Find angular velocity of the system immediately after after the collision about O.
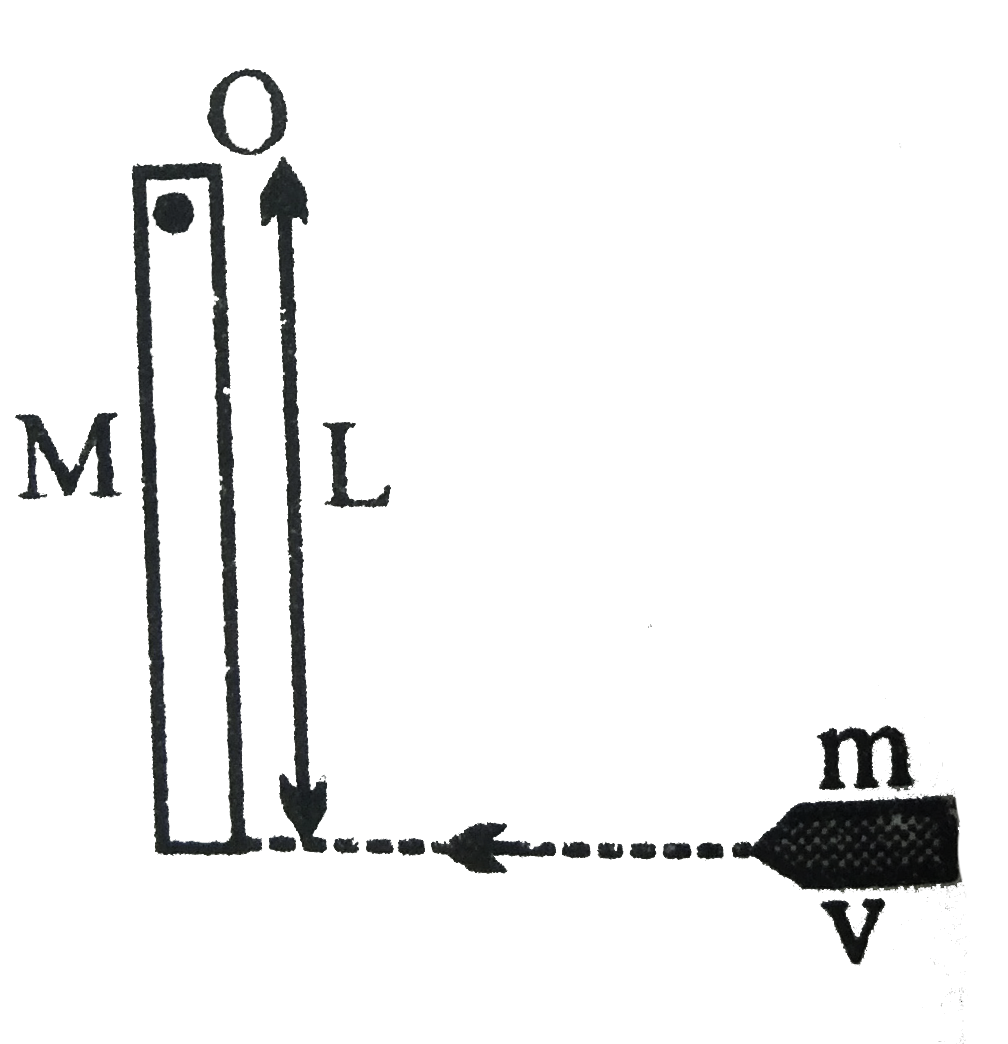 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
A rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
A3√2V7LB√2V7LC√2V3LD3V7L - Question 2 - Select One
A uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 A6v05LB12v05LC2v05LD3v07L
A6v05LB12v05LC2v05LD3v07L - Question 3 - Select One
A bag of mass M hangs by a long massless rope. A bullet of mass in, moving horizontally with velocity u, is caught in the bag. Then for the combined (bag + bullet) system, just after collision
Amomentum is muM/(M+m)Bkinetic energy is mu2/2Cmomentum is mu(M+m)/MDkinetic energy is m2u2/2(M+m)
A particle of mass m strikes another particle of same at rest. Find the angle between velocities of particles after the collision , if the collision is elastic.
View SolutionA rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end. A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod
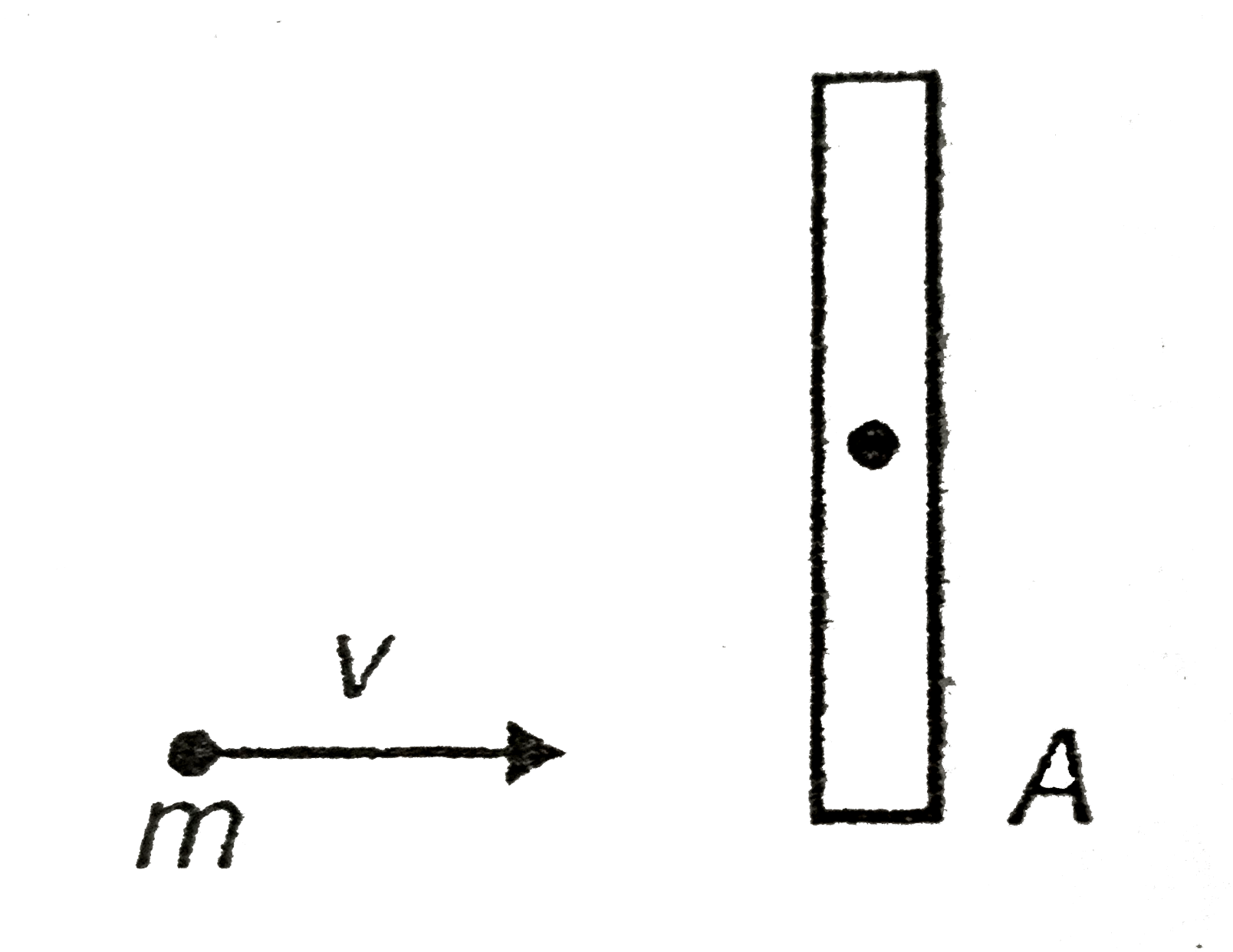 View Solution
View SolutionA rod of mass m and length L is kept on a frictionless horizontal floor. A particle of same mass m moving perpendicular to the rod with a speed v strikes at the end of the rod. If coefficient of elasticity for the collision is 1 then calculate angular velocity acquired by the rod.
View SolutionA circular wooden hoop of mass m and radius R rests fiat on a frictionless surface. A bullet, also of mass m and moving with a velocity v, strikes the hoop and gets embedded in it. The thickness of the hoop is much smaller than R. Find the angular velocity with which the system rotates in after the bullet strikes the hoop.
 View Solution
View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View Solution

