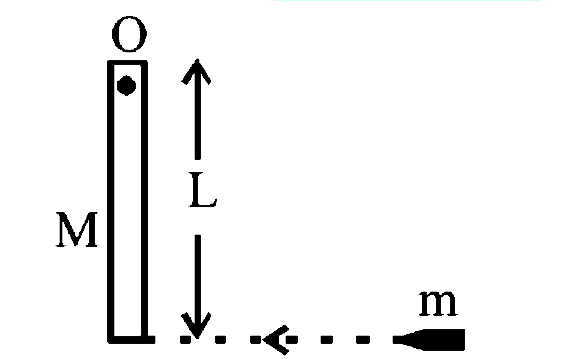
A wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.
The correct Answer is:A, C
We know that τ=dvacLdt
τ×dt=d→L
when angular impulse (τ×d→t) is zero, the anglar
momentum is constant. In this case for the wooden
log-bullet system the angular impulse about O is constant .
therefore.
[anga––rmomentumofthesystem]∈itial
=[anga––rmomentumofthesystem]∈ital
⇒mv×L=I0×ω.....(i)
where I0 is the moment of inertia of the wooden log - bullet
system after collision aobut O
I0=Iw∞denlog+Ib≤–––t
=13ML2+ML2....(ii)
From (i) and (ii)
ω=mv×L[13ML2+mL2]
⇒oemga=mvML3+mL⎤⎦ = (3mv)/((M+3m))L)
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
A wooden log of mass M and length L is hinged by a frictionless nail at O. A bullet of mass m strikes with velocity v and sticks to it. Find the angular velocity of the system, immediately after the collision about O. Also, calculate the minimum value of v so that log becomes horizontal after collision.
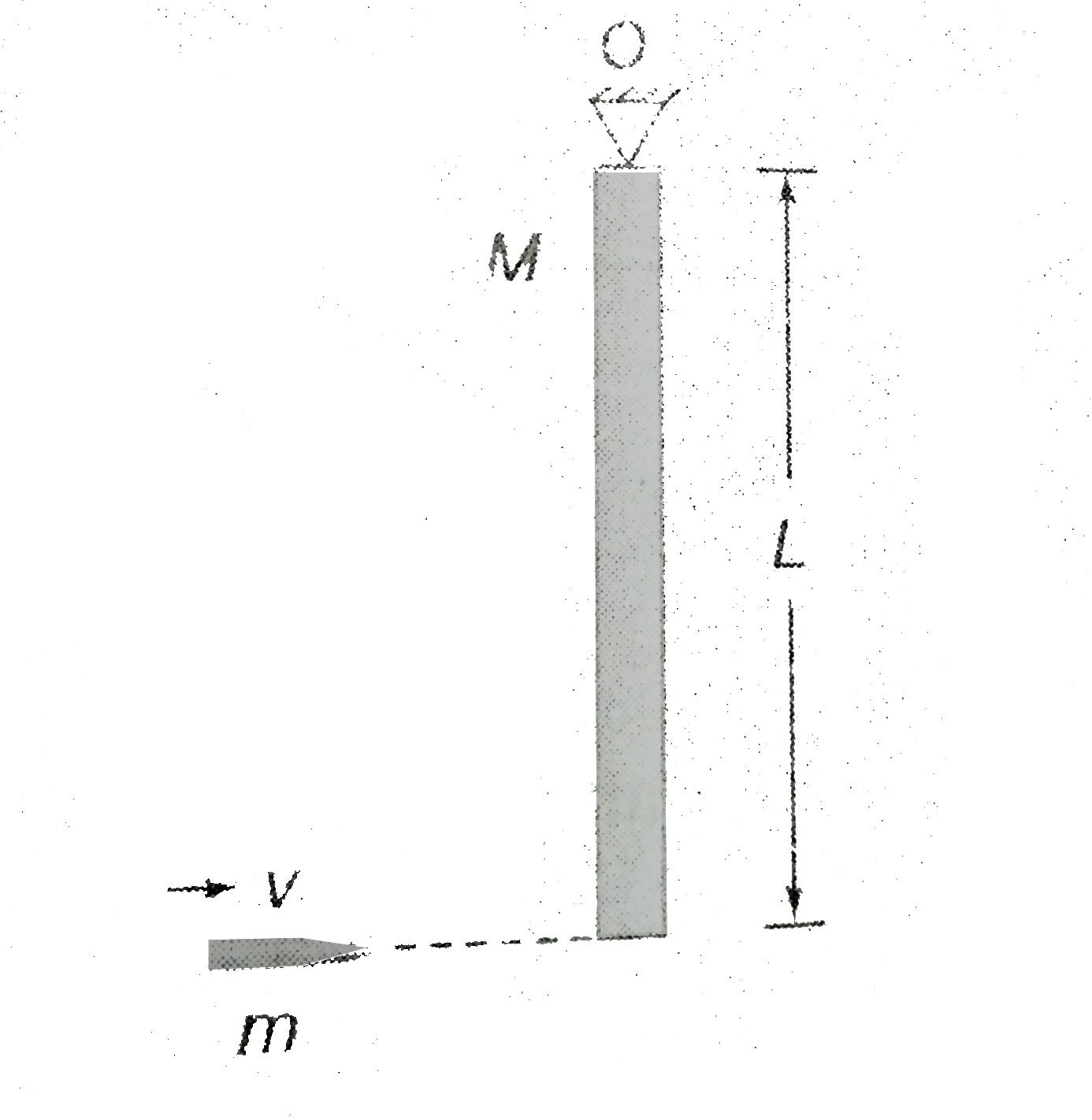
View SolutionA wodden log mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and strikes with velocity v and sticks to it . Find angular velocity of the system immediately after after the collision about O.
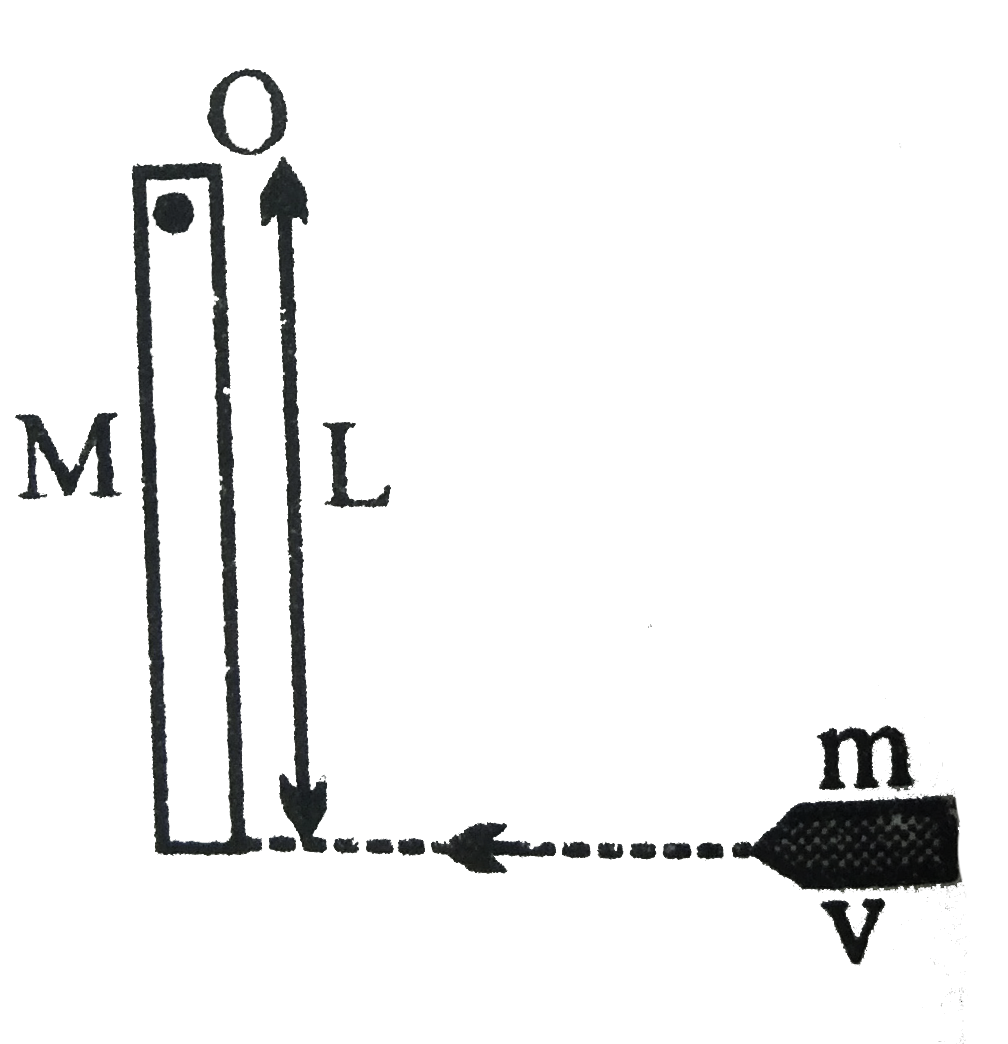 .
.
View Solution
Knowledge Check
A bullet of mass A and velocity B is fried into a block of mass C and sticks to it. The final velocity of the system equals
AA+BCABAA+CBCA+CBDAA+BBA bullet of mass m is fired with velocity v in a large bulk of mass M. The final velocity v' will be
AMvm+MBmvm+MC(m+M)vmD(m+M)vA bullet of mass m is fired with velocity v in a large bulk of mass M. The final velocity v' will be
AMvm+MBmvm+MC(m+M)mmD(m+M)v
A rod of mass m,length l pivoted at its centre is free to rotate in a vertical plane.The rod is at rest and is in vertical position.A bullet of mass m/2 moving horizontally with speed v strikes and sticks to one end of the rod. Angular velocity of system just after collision is
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
View SolutionA body of mass a moving with a velocity b strikes a body of mass c and gets embered into it. The velocity of the systems after collision is
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View Solution
