Question

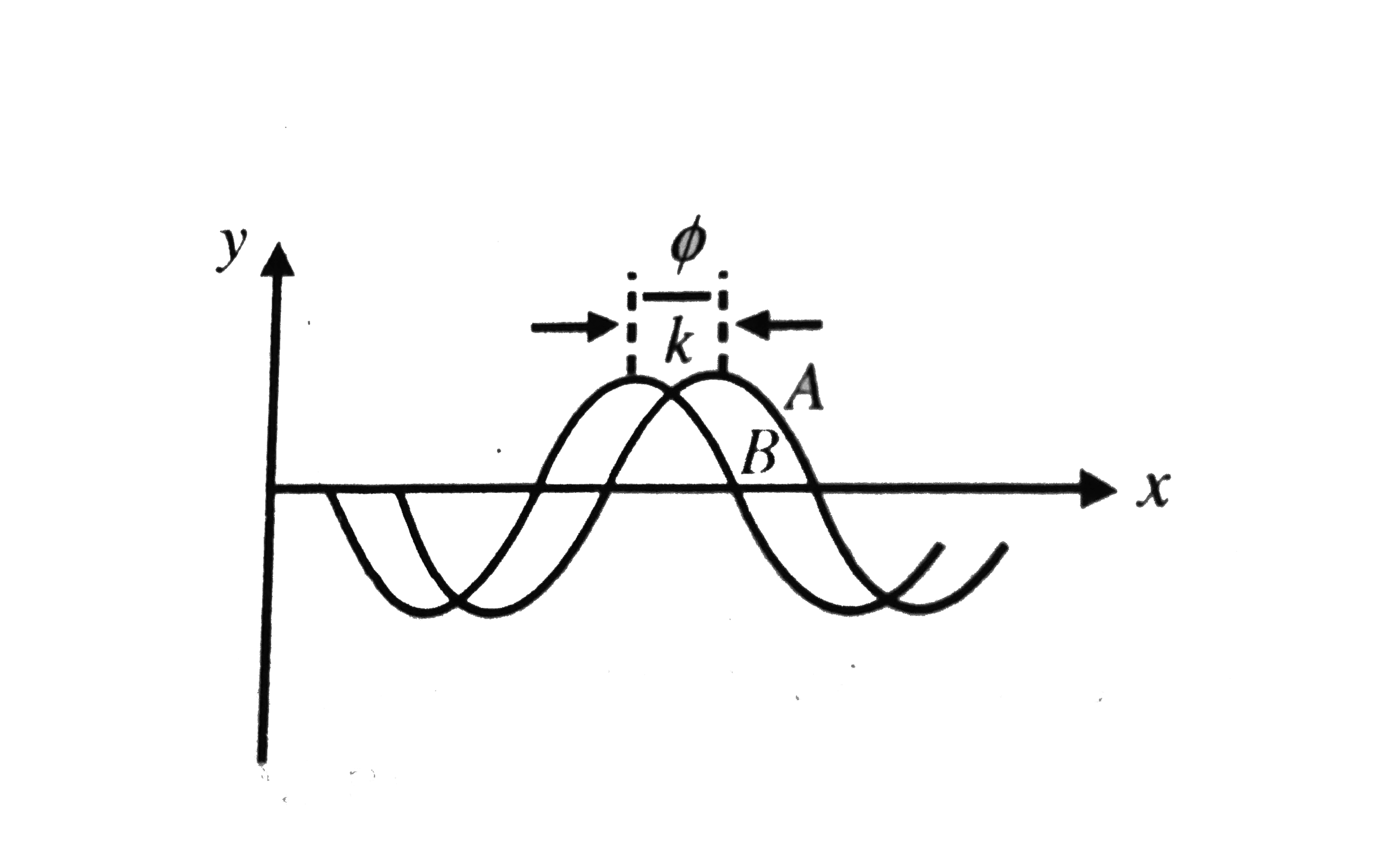
Adjoining figure shows the snapshot of two waves A and B at any time t. the equation for A is $y=A\sin (kx-\omega t-\varphi )$, and for B it is $y=A\sin (kx-\omega t)$. It is clearly shown in the figure that wave A is ahead of B by a distance $\varphi /k$.

Options

A.
B.
C.
D.

Answer

b

Explanation

The equation for wave A can be rewritten as
`y=A sin[kx-omegat-phi]`
`=A sin[k(x-phi//k)-omegat]`
`A sin[kx-omega(t+(phi)/(k))]`
while equation of wave `B` is `y= A sin (kx-omegat)`.
Comparing above equation, we can easily conclude that `A` is at a distance ahead of `phi//k` from `B` or wave `A` is ahead of `B` by a time difference of `phi//omega`.So, (b) is the correct option.
Remember `!` In y versust'ahead of means to the left of' while in `y` versus `x` 'ahead of means to the right of' if the wave travels in positive `x-`direction and vice versa.