After falling from rest through a height h, a body of mass m begins to raise a body of mass M(M>m) connected to it through a pulley. Determnethe time it will take for the body of mass M to return to its original position
2mMm√2hg
2mM−m√2hg
2mM−m√hg
mM−m√2hg
The correct Answer is:B
To solve the problem, we will break it down into steps:
Step 1: Determine the speed of mass m just before the string becomes taut.
When the mass m falls from rest through a height h, we can use the equation of motion to find its speed just before the string becomes taut. The equation is given by:
\(
v = \sqrt{2gh}
\)
Step 2: Apply conservation of momentum at the moment the string becomes taut.
At the moment the string becomes taut, the momentum of the system must be conserved. Let V' be the common speed of both masses m and M after the string is jerked. The conservation of momentum gives us:
\(
mv = (M + m)V'
\)
Substituting for v from Step 1, we have:
\(
m\sqrt{2gh} = (M + m)V'
\)
From this, we can solve for V':
\(
V' = \frac{m\sqrt{2gh}}{M + m}
\)
Step 3: Determine the acceleration of the system.
The net force acting on the system when the mass M is rising and mass m is falling is given by:
\(
F = Mg - mg
\)
Using Newton's second law:
\(
F = (M + m)a
\)
Setting these equal gives:
\(
Mg - mg = (M + m)a
\)
From this, we can solve for a:
\(
a = \frac{Mg - mg}{M + m} = \frac{(M - m)g}{M + m}
\)
Step 4: Use the kinematic equation to find the time t taken for mass M to return to its original position.
We use the kinematic equation:
\(
S = ut + \frac{1}{2}at^2
\)
Since mass M returns to its original position, the displacement S is equal to 0, and the initial velocity u is equal to V'. Thus, we have:
\(
0 = V't - \frac{1}{2}at^2
\)
Rearranging gives:
\(
\frac{1}{2}at^2 = V't
\)
Dividing both sides by t (assuming t≠0):
\(
\frac{1}{2}at = V'
\)
From this, we can solve for t:
\(
t = \frac{2V'}{a}
\)
Step 5: Substitute for V' and a to find t.
Substituting the expressions for V' and a from Steps 2 and 3:
\(
t = \frac{2 \left(\frac{m\sqrt{2gh}}{M + m}\right)}{\frac{(M - m)g}{M + m}}
\)
This simplifies to:
\(
t = \frac{2m\sqrt{2h}}{(M - m)\sqrt{g}}
\)
Final Result
Thus, the time it will take for the body of mass M to return to its original position is:
\(
t = \frac{2m\sqrt{2h}}{(M - m)\sqrt{g}}
\)
---
When the mass m falls from rest through a height h, we can use the equation of motion to find its speed just before the string becomes taut. The equation is given by:
v = \sqrt{2gh}
\)
At the moment the string becomes taut, the momentum of the system must be conserved. Let V' be the common speed of both masses m and M after the string is jerked. The conservation of momentum gives us:
mv = (M + m)V'
\)
m\sqrt{2gh} = (M + m)V'
\)
V' = \frac{m\sqrt{2gh}}{M + m}
\)
The net force acting on the system when the mass M is rising and mass m is falling is given by:
F = Mg - mg
\)
F = (M + m)a
\)
Mg - mg = (M + m)a
\)
a = \frac{Mg - mg}{M + m} = \frac{(M - m)g}{M + m}
\)
We use the kinematic equation:
S = ut + \frac{1}{2}at^2
\)
0 = V't - \frac{1}{2}at^2
\)
\frac{1}{2}at^2 = V't
\)
\frac{1}{2}at = V'
\)
t = \frac{2V'}{a}
\)
Substituting the expressions for V' and a from Steps 2 and 3:
t = \frac{2 \left(\frac{m\sqrt{2gh}}{M + m}\right)}{\frac{(M - m)g}{M + m}}
\)
t = \frac{2m\sqrt{2h}}{(M - m)\sqrt{g}}
\)
Thus, the time it will take for the body of mass M to return to its original position is:
t = \frac{2m\sqrt{2h}}{(M - m)\sqrt{g}}
\)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
After falling from rest through a height h, a body of mass m begins to raise a body of mass M(M>m) connected to it through a pulley.
Find the fraction of kinetic energy lost when the body of mass M is jerked into motion
View SolutionThe horizontal component of the weight of a body of mass m is
View Solution
Knowledge Check
Body 1 of mass M is dropped from a height of 1 m and body 2 of mass 3 M is dropped from a height of 9 m. Ratio of time taken by bodies 1 and 2 to reach the ground is
A1:1B1:3C3:1D9:1
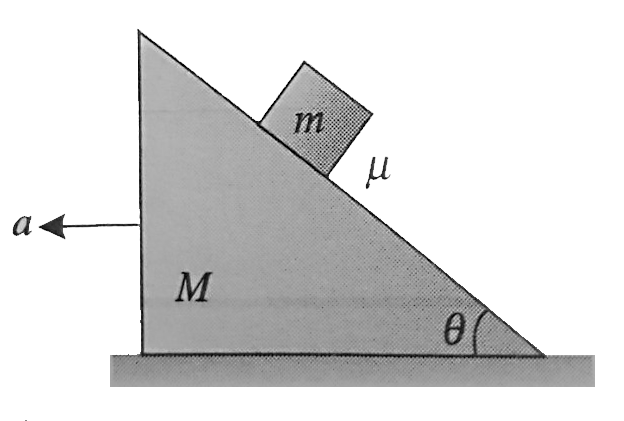
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
View SolutionTwo bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.

View SolutionIf a body of mass m is raised to height 2 R from the earths surface, then the change in potential energy of the body is (R is the radius of earth)
View SolutionA body of mass 5 kg is raised vertically to a height of 10 m by a force 170 N. The velocity of the body at this height will be
View SolutionA body of mass m moving with velocity 3km/h collides with a body of mass 2m at rest. Now, the combined mass starts to move with a velocity
View SolutionA body of mass 10 kg moving at a height of 2 m, with uniform speed of 2 m/s. Its total energy is
View SolutionCalculate the increase in mass when a body of rest mass 1 kg is lifted up through 1 m near the earth's surface.
View Solution