Air is filled inside a jar which has a pressure gauge connected to it. The temperature of the air inside the jar is same as outside temperature (=T0) but pressure (P1) is slightly larger than the atmospheric pressure (P0). The stopcock is quickly opened and quickly closed, so that the pressure inside the jar becomes equal to the atmospheric pressure P0. The jar is now allowed to slowly warm up to its original temperature T0. At this time the pressure of the air inside is P2(P0<P2<P1). Assume air to be an ideal gas. Calculate the ratio of specific heats (=γ) for the air, in terms of P0,P1 and P2.
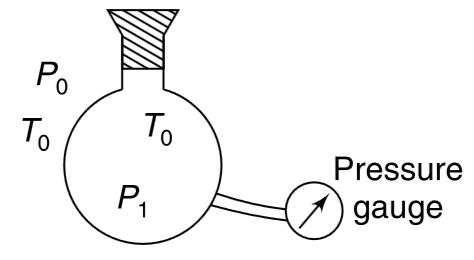
The correct Answer is:γ=ln(P0/P1)ln(P2/P1)
Step by step video, text & image solution for Air is filled inside a jar which has a pressure gauge connected to it. The temperature of the air inside the jar is same as outside temperature (= T_(0)) but pressure (P_(1)) is slightly larger than the atmospheric pressure (P_(0)). The stopcock is quickly opened and quickly closed, so that the pressure inside the jar becomes equal to the atmospheric pressure P_(0). The jar is now allowed to slowly warm up to its original temperature T_(0). At this time the pressure of the air inside is P_(2) (P_(0) lt P_(2) lt P_(1)). Assume air to be an ideal gas. Calculate the ratio of specific heats (= gamma) for the air, in terms of P_(0), P_(1) and P_(2). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
- ELASTICITYBOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 3
1 Videos
- FLUIDSBOOK - ARIHANTCHAPTER - FLUIDSEXERCISE - All Questions
70 Videos
Similar Questions
Knowledge Check
The temperature, at which the vapour pressure of a liquid becomes equal to the atmospheric pressure is known as
AFreezing pointBBoiling pointCAbsolute temperatureDNormal temperatureThe temperature, at which the vapour pressure of a liquid becomes equal to the atmospheric pressure is known as
AFreezing pointBBoiling pointCAbsolute temperatureDNone of theseThe temperature, at which the vapour pressure of a liquid becomes equal to the atmospheric pressure is known as
AFreezing pointBBoiling pointCAbsolute temperatureDNone of these
The temperature at which the vapour pressure of liquid becomes equal to atmospheric pressure is called
View SolutionHow does the speed v of sound in air depend on the atmospheric pressure P?
View SolutionAn air bubble is formed at depth h below the surface of water. The pressure inside the bubble is-
(P0= atmospheric pressure, r = radius of bubble)
View SolutionAssertion : In the given figure shown, p1=p2.
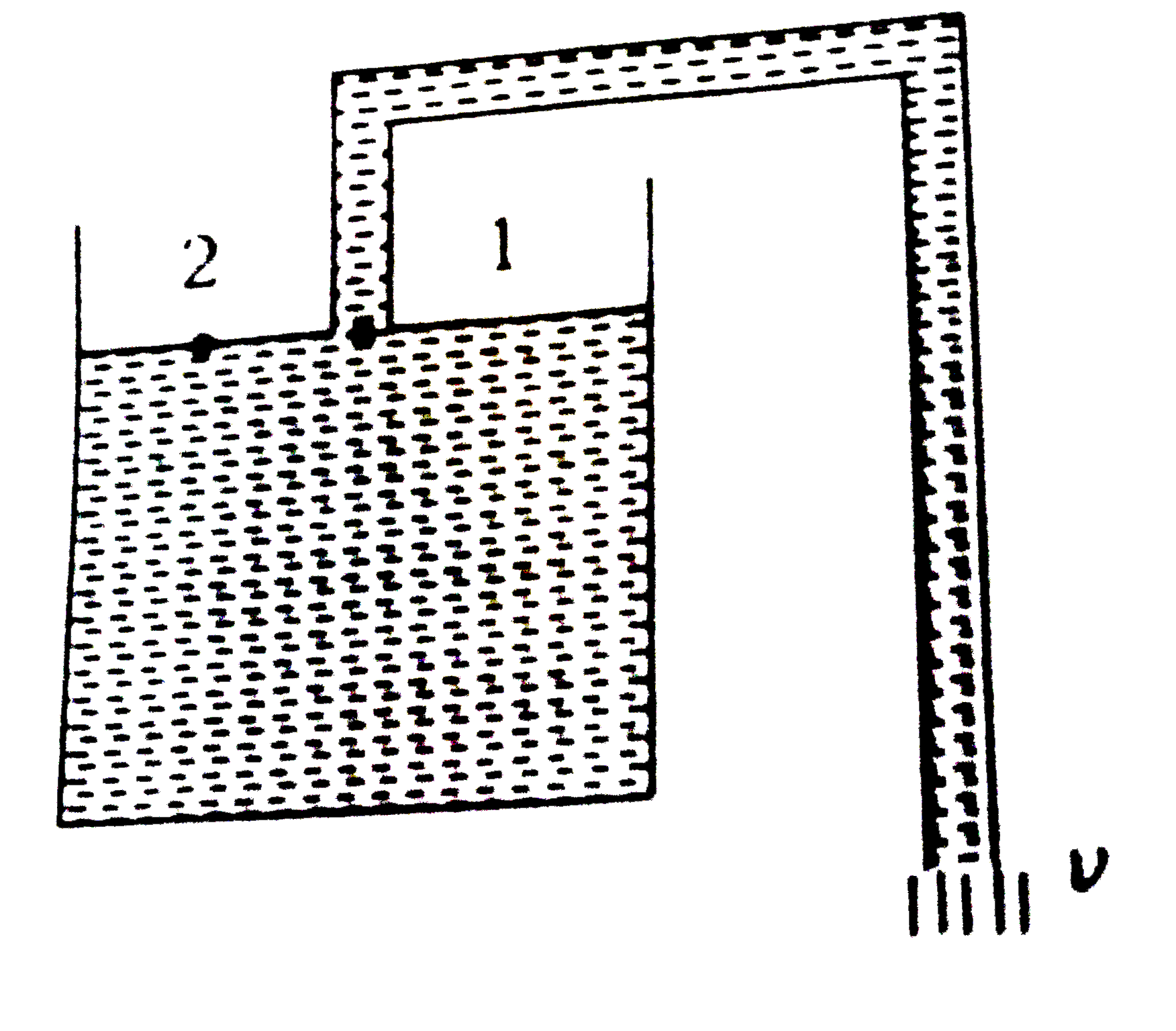
Reason : Pressure at 1 is less than the atmospheric pressure.
View SolutionHow does the speed V of sound in air depend on atmospheric pressure P ?
View Solution

