All the string in figure are massless. Tension in the horizontal string is 30N. Find W.
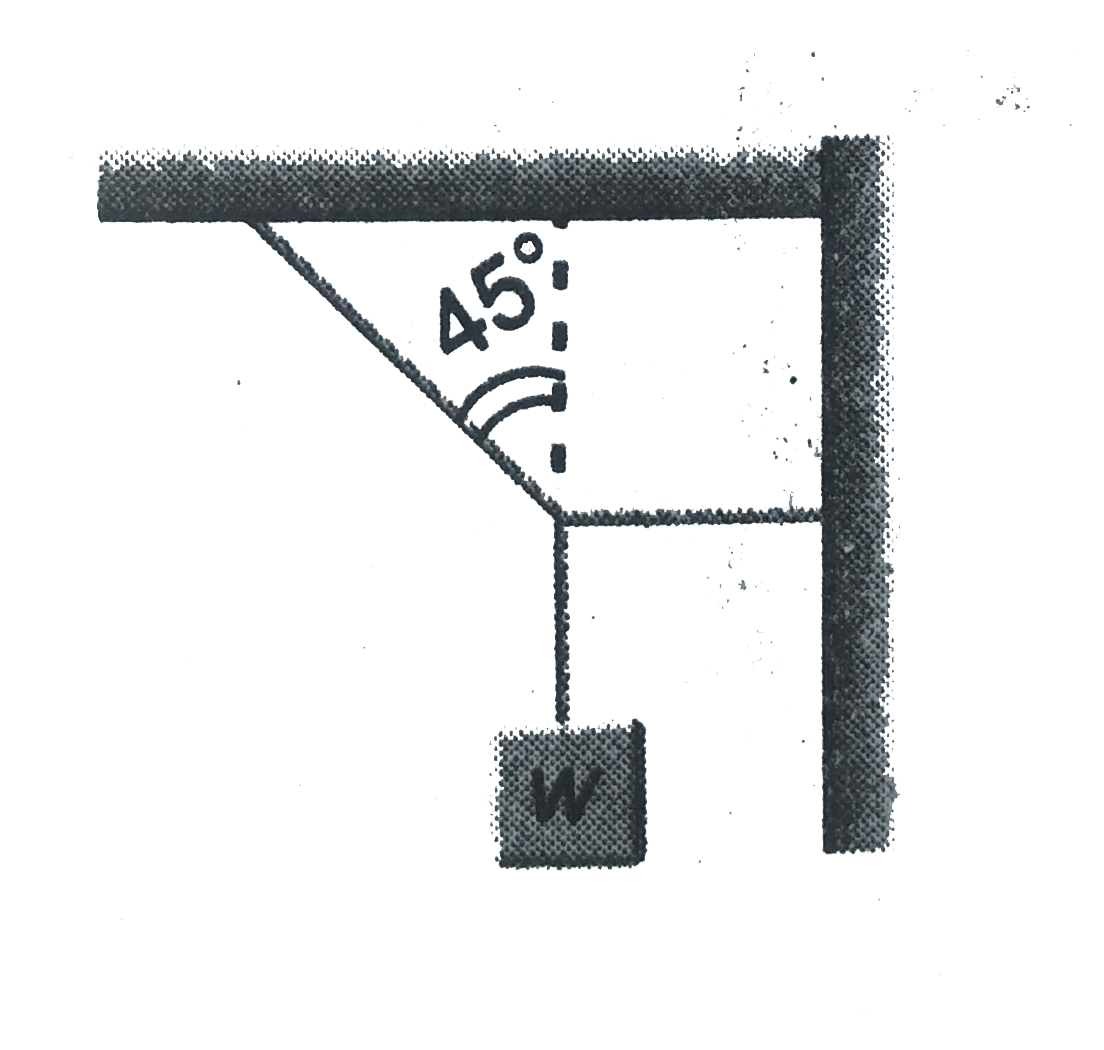
Video Solution
Text Solution
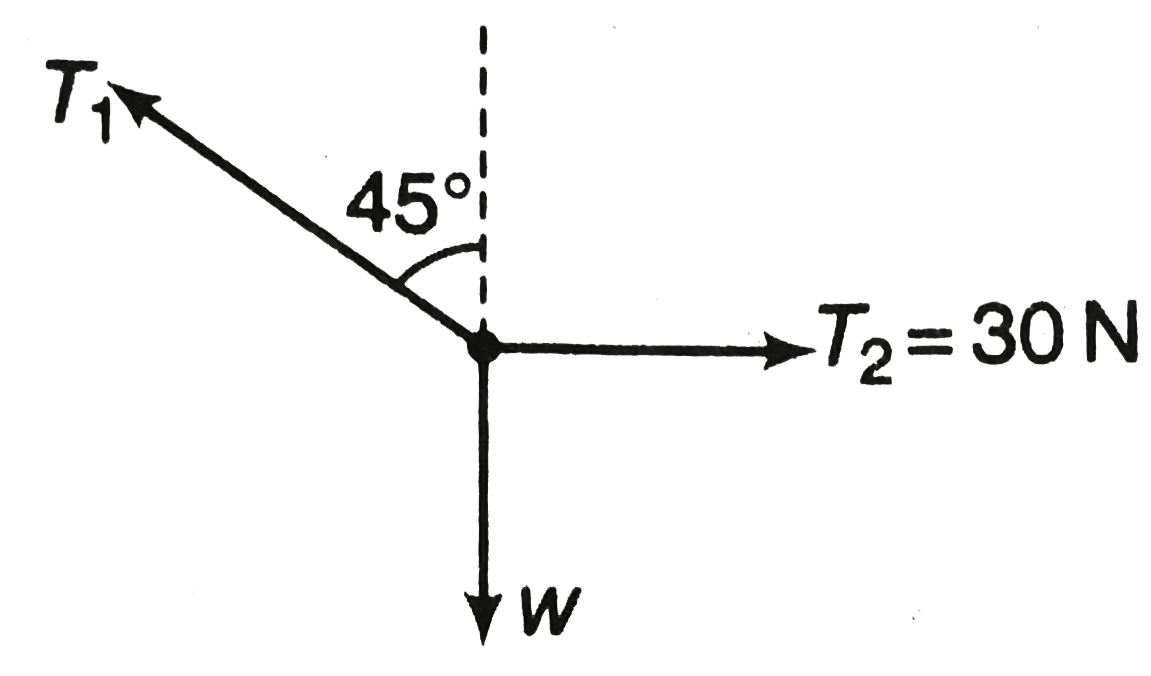
T1cos45∘=w
and T1sin45∘=30N
|
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.2
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.3
8 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Miscellaneous Examples
9 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Knowledge Check
As shown in figure the tension in the horizontal cord is 30N. The weight W and tension in the string OA in Newton are
 A30√3,30B30√3,60C60√3,30DNone of these
A30√3,30B30√3,60C60√3,30DNone of theseA bob in tied to a string of length l & and kept on a horizontal rough surface as shown in the figure when point O of the string is fixed. The bob is given a tangential velocity V0 keeping the string taut as shown in figure. Find the tension in the string as a function of time. The coefficient of kinetic friction is μ.
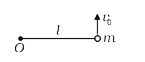 Am(v0−μgt)2/1Bm(v0+μgt)2/1Cm(v0+>)2/1Dm(v0−>)2/1
Am(v0−μgt)2/1Bm(v0+μgt)2/1Cm(v0+>)2/1Dm(v0−>)2/1A mass M is hung with a light inextensible string. Tension in horizontal part of string is.
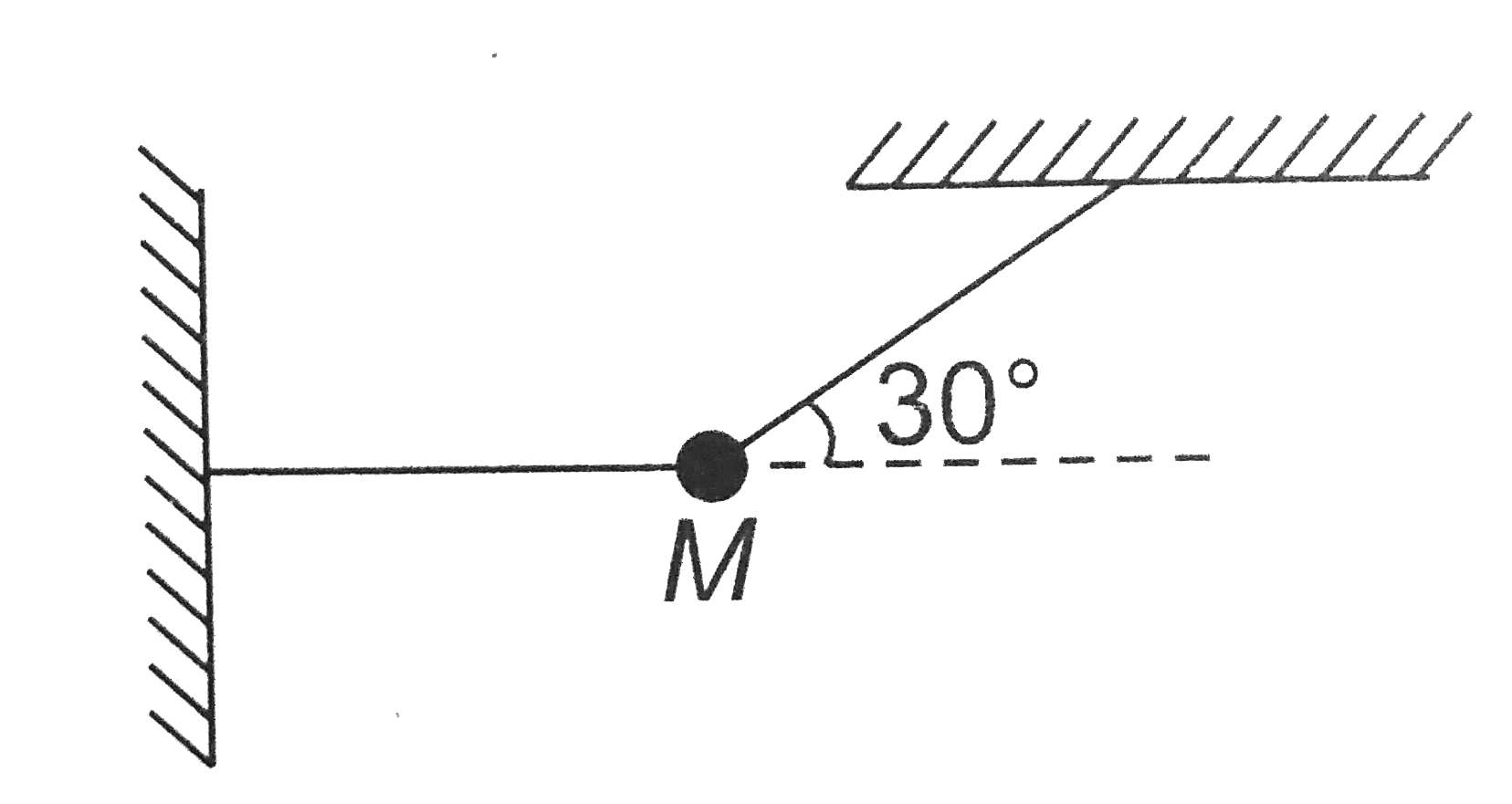 A√3MgB√2MgCmg√3Dmg2
A√3MgB√2MgCmg√3Dmg2
In the adjoining figure, the tension in the string connecting A and B is :-
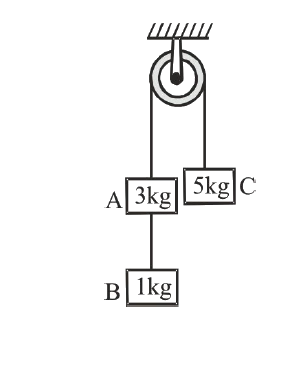
View SolutionThe tension T in the string shown in figure is

View SolutionA mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
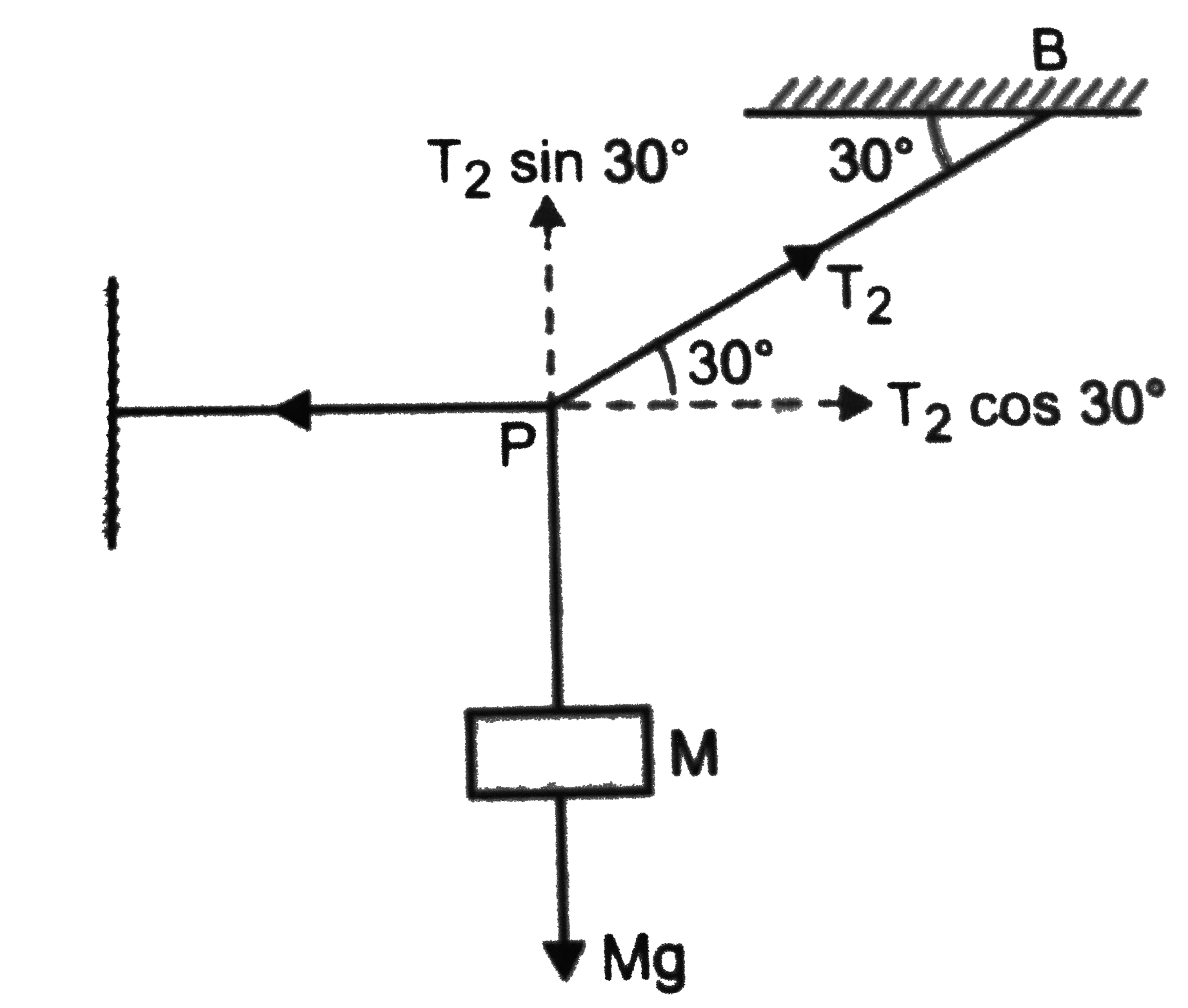
View SolutionPulleys and strings are massless. The horizontal surface is smooth. What is the acceleration of the block

View SolutionA mass is supported on a frictionless horizontal surface. It Is attached to a string and rotates about a fixed center at an angular velocity ω0.If the length of the string and angular velocity both are doubled, the tension in the string which was initially T0 is now
View Solution