An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U=1.5nRT) and the part on the right contains two moles of the same gas. initially, the pressure on each side is p. the system is left for sufficient time so that a steady state is reached. find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c ) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
The correct Answer is:A, B, C, D
To solve the problem step by step, we will analyze each part of the question systematically.
Given Data:
- Total volume V divided into two equal parts: V1=V2=V2
- Left part contains 1 mole of ideal gas, right part contains 2 moles of the same gas.
- Initial pressure on both sides is P.
- Internal energy of the gas is given as U=1.5nRT.
(a) Work done by the gas in the left part during the process
Since the separator is fixed, there is no change in volume for the gas in the left part. Therefore, the work done W can be calculated as:
W=PΔV
Here, ΔV=0 (no change in volume), so:
W=P⋅0=0
Thus, the work done by the gas in the left part is 0.
(b) Temperature on the two sides in the beginning
Using the ideal gas law PV=nRT, we can find the initial temperatures for both sides.
For the left part:
PV1=n1RT1⟹P⋅V2=1⋅R⋅T1⟹T1=PV2R
For the right part:
PV2=n2RT2⟹P⋅V2=2⋅R⋅T2⟹T2=PV4R
(c) Final common temperature reached by the gases
The total internal energy before the process can be calculated as:
Utotal=Uleft+Uright=n1CvT1+n2CvT2
Using Cv=3R2 for an ideal gas:
Uleft=1⋅3R2⋅T1=3R2⋅PV2R=3PV4
Uright=2⋅3R2⋅T2=3R⋅PV4R=3PV4
Thus,
Utotal=3PV4+3PV4=3PV2
The final temperature Tf can be calculated using:
Utotal=ntotalCvTf⟹3PV2=3⋅3R2⋅Tf
Solving for Tf:
Tf=PV3R
(d) Heat given to the gas in the right part
Using the first law of thermodynamics:
dQ=dU+dW
Since dW=0:
dQ=dU
The change in internal energy for the right part is:
dUright=n2Cv(Tf−T2)=2⋅3R2(PV3R−PV4R)
Calculating:
=3(PV3R−PV4R)=3(4PV−3PV12R)=PV4
(e) Increase in the internal energy of the gas in the left part
The change in internal energy for the left part is:
dUleft=n1Cv(Tf−T1)=1⋅3R2(PV3R−PV2R)
Calculating:
=3R2(2PV−3PV6R)=3R2⋅(−PV6R)=−PV4
Summary of Answers:
(a) Work done by the gas in the left part: 0
(b) Initial temperature on the left: T1=PV2R
Initial temperature on the right: T2=PV4R
(c) Final common temperature: Tf=PV3R
(d) Heat given to the gas in the right part: PV4
(e) Increase in the internal energy of the gas in the left part: −PV4
- Total volume V divided into two equal parts: V1=V2=V2
- Left part contains 1 mole of ideal gas, right part contains 2 moles of the same gas.
- Initial pressure on both sides is P.
- Internal energy of the gas is given as U=1.5nRT.
Since the separator is fixed, there is no change in volume for the gas in the left part. Therefore, the work done W can be calculated as:
W=PΔV
Here, ΔV=0 (no change in volume), so:
W=P⋅0=0
Thus, the work done by the gas in the left part is 0.
Using the ideal gas law PV=nRT, we can find the initial temperatures for both sides.
PV1=n1RT1⟹P⋅V2=1⋅R⋅T1⟹T1=PV2R
PV2=n2RT2⟹P⋅V2=2⋅R⋅T2⟹T2=PV4R
The total internal energy before the process can be calculated as:
Utotal=Uleft+Uright=n1CvT1+n2CvT2
Using Cv=3R2 for an ideal gas:
Uleft=1⋅3R2⋅T1=3R2⋅PV2R=3PV4
Uright=2⋅3R2⋅T2=3R⋅PV4R=3PV4
Thus,
Utotal=3PV4+3PV4=3PV2
The final temperature Tf can be calculated using:
Utotal=ntotalCvTf⟹3PV2=3⋅3R2⋅Tf
Solving for Tf:
Tf=PV3R
Using the first law of thermodynamics:
dQ=dU+dW
Since dW=0:
dQ=dU
The change in internal energy for the right part is:
dUright=n2Cv(Tf−T2)=2⋅3R2(PV3R−PV4R)
Calculating:
=3(PV3R−PV4R)=3(4PV−3PV12R)=PV4
The change in internal energy for the left part is:
dUleft=n1Cv(Tf−T1)=1⋅3R2(PV3R−PV2R)
Calculating:
=3R2(2PV−3PV6R)=3R2⋅(−PV6R)=−PV4
(a) Work done by the gas in the left part: 0
(b) Initial temperature on the left: T1=PV2R
Initial temperature on the right: T2=PV4R
(c) Final common temperature: Tf=PV3R
(d) Heat given to the gas in the right part: PV4
(e) Increase in the internal energy of the gas in the left part: −PV4
Topper's Solved these Questions
Similar Questions
An insulting container of volume 2V0 is divided in two equal parts by a diathermic (conducting) fixed piston. The left part contains one mole of monoatomic ideal gas whereas right part contains two moles of the same gas. Initial pressue on each side is P0. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) initial temperature in the two sides, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
View SolutionA vessel of volume V is divided into two parts by a partition. The pressure of the gas in one part is p1 and that in the other part is p2. If the partition is removed find the pressure of the gas in the vessel.
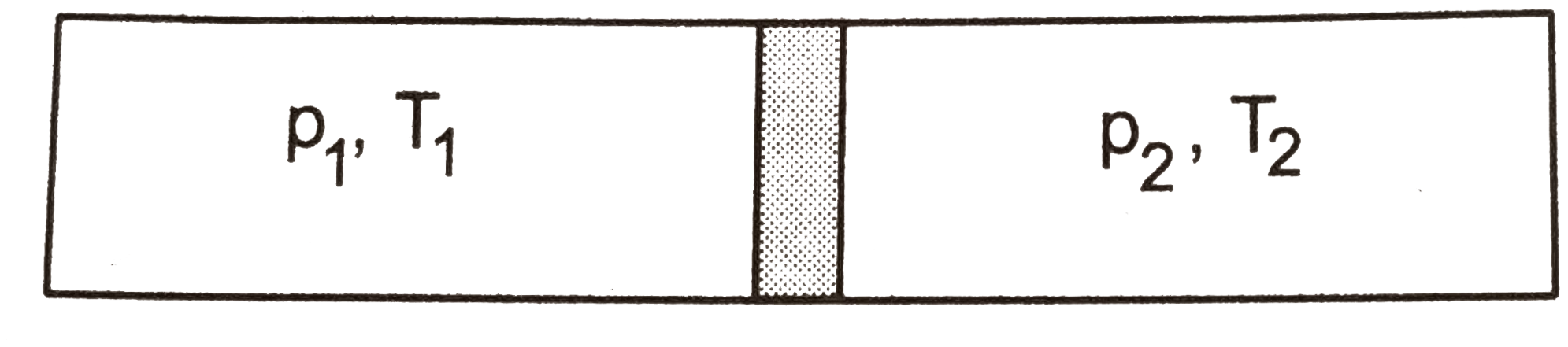
View SolutionFig shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1,T1 on the left and p2,T2 on the right. the system is left for sufficient time so that the temperature becomes equal on the two sides. (a) how much work has been done by the gas on the left part ? (b) find the final pressures on the two sides. (c ) find the final equilibrium temperature. (d) how much heat has flown from the gas on the right to the gas on the left ?
View SolutionA cylindrical vessel made of thermally insulating material is divided into two equal parts by an insulating and. Movable piston. Both parts contain ideal monoatomic gas . The gas in the left part is supplied heat such that the volume of right part becomes one-eight of its initial volume . Work done by the gas in the right part is
View SolutionFigure shows an adiabatic cylindrical tube of volume (V0) divided in two parts by a frictionless adiabatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (P1) and the temperatures (T1) is injected into the left part and the another ideal gas at pressures (P2) and temperature (T2) is injected into the right part. (CpCv=γ) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find
(a) the volumes of the parts,
(b) the heat given to the gas in the left part and
(c) the final common pressure of the gases.

View SolutionIn given figure, an adiabatic cylindrical tube of volume 2V0 is divided in two equal parts by a frictionless adiabatic separator. An ideal gas in left side of a tube having pressure P1 and temperature T1 where as in the right side having pressure P2 and temperature T2.Cp/Cv=γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the final volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases,
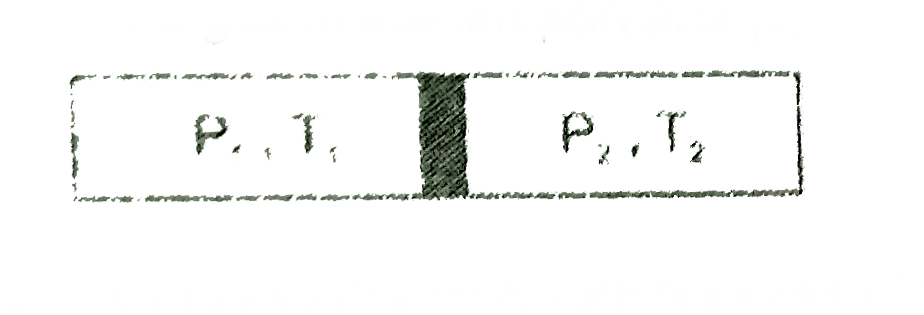
View SolutionA container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated . If the valve is suddenly opened, the pressure and temperature of the gas will be
View SolutionA container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated . If the valve is suddenly opened, the pressure and temperature of the gas will be
View SolutionOne mole of an ideal gas has an interal energy given by U=U0+2PV , where P is the pressure and V the volume of the gas. U0 is a constant. This gas undergoes the quasi− static cyclic process ABCD as shown in the U−V diagram. The work done by the ideal gas in the process AB is

View SolutionA cylindrical adiabatic container of total volume 2V0 divided into two equal parts by a conducting piston which is free to move as shown in figure. Each part containing identical gas at pressure P0. Initially temperature of left and right part is 4T0andT0 respectively. An external force is applied on the piston of area 'A' to keep the piston at rest. The value of external force required when thermal equilibrium is reached is.
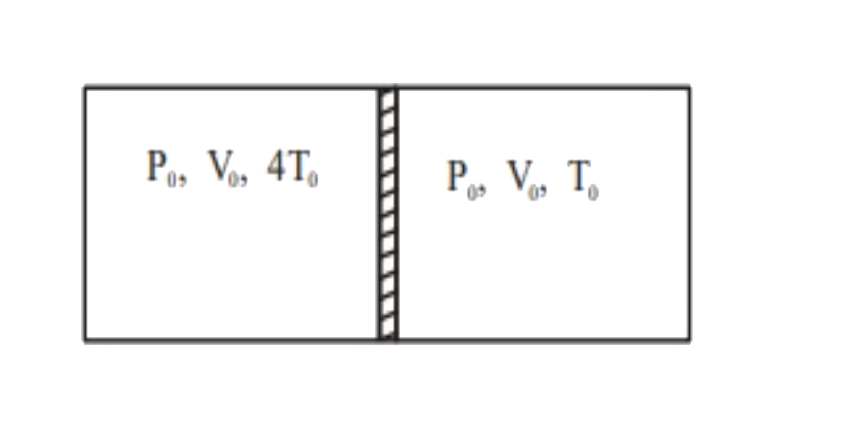
View Solution
