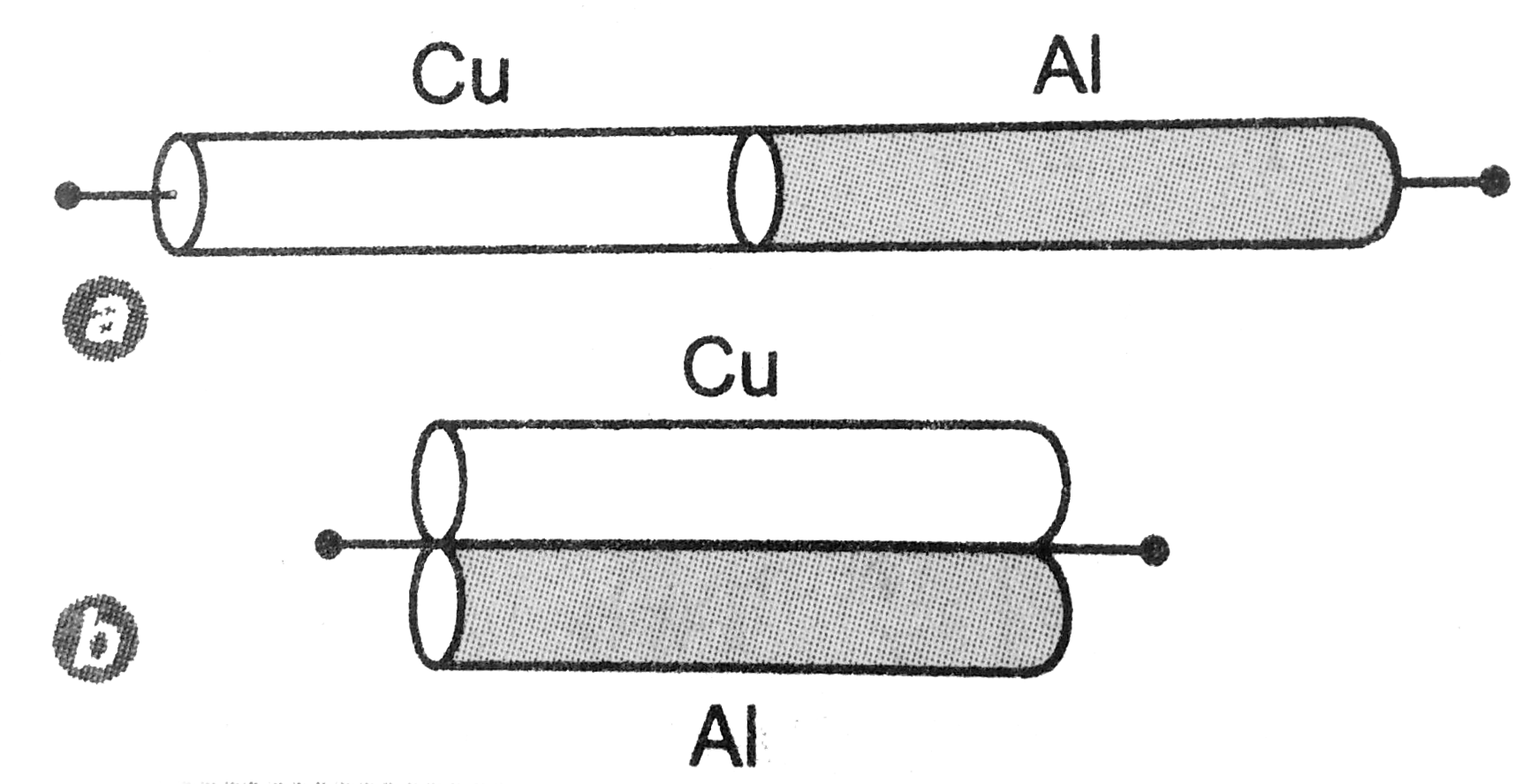
An aluminium rod and copper rod of equal length 1m and cross-sectional area 1cm2 are welded as shown. KA1=200W/m∘C,KCu=400W/m∘C. Find heat current


RA1=lKA1A=l200×10−4=50∘C/W
RCu=lKCuA=1400×10−4=25∘C/W
(a) Req=RA1+RCu=50+25=75∘C/W
Heat current i=100−25Req=7575=1W
(b) Req=RA1.RCuRA1+RCu=50×2550+25=503.∘C/W
Heat current i=100−2550/3=4.5W
Topper's Solved these Questions
Similar Questions
An aluminium rod and a copper rod of equal length 1.0m and cross-sectional area. 1cm2 are welded together as shown in figure. One end is kept at a temperature of 20∘C and the other at 60∘C Calculate the amount of heat taken out per second from the hot end. thermal conuctivity of aluminium =200Wm−1^(@)C^(-1)andofcopper=390Wm^(-1)^(∘)C−1 .

View SolutionTwo rods of copper and aluminium of each of equal length 20 cm and equal cross-sectional area 2mm2. They are joined (i) in series and (ii) in parallel as shown in figure. Find the resistance of the combination in each case. Resistivity of copper =1.7×10−8Ωm and resistivity of aluminium =2.6×10−8Ωm.
View Solution
Knowledge Check
The ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK
 AThe temperature of rod at centre is 250∘CBThe temperature of rod at centre is 50∘CCThe temperature gradient in right half is 500∘C/mDThe temperature gradient in left half is 300∘C/m
AThe temperature of rod at centre is 250∘CBThe temperature of rod at centre is 50∘CCThe temperature gradient in right half is 500∘C/mDThe temperature gradient in left half is 300∘C/m
A metal frame of total length 50cm ad croos-sectional area 0.20cm2 froms five sides of a regular hexagon. The free ends are maintained at 20∘C and 40∘C. Find the rate of heat flow through a cross-section of the frame (K=50W/m∘C)
View Solution(a) Three rod of lengths 20cm each and area of cross-section 1cm2 are joined to form a triangle ABC. The conductivities of the rods are KAB=50J/m−s−.∘C,KBC=200J/m−s−.∘C and KAC=400J/m−s−.∘C. The junctions A,B and C are maintained at 40∘C, 80∘C and 80∘C respectively. Find the rate of heat flowing through the rods AB,AC and BC.
(b) A semicircular rod is joineted as its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross-section of the simicircular rod to the heat transferred through a cross-section of the straight rod in a given time.
View SolutionA copper rod of length 20 cm and cross-sectional area 2mm2 is joined with a similar aluminium rod as shown in Fig. 4.6. Find the resistance of the combination between the ends. Resistivity of copper =1.7×10−8Ωm and resistivity of aluminium =2.6×10−8Ωm.

View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionA copper rod of length 20cm and cross-sectional area 2mm2is joined with a similar aluminium rod as shown in figure .Find the resistance of the combination between the ends, Resistivity of copper =1.7×10−8(Ω)mand that of aluminium=2.6×10−8(Ω)m.

View SolutionThree copper rods and three steel rods each of length l=10cm and area of cross-section 1cm2 are connected as shown

If ends A and E are maintained at temperatures 125∘C and 0∘C respectively, calculate the amount of heat flowing per second from the hot of cold function. [KCu=400W/m−K,Ksteel=50W/m−K]
View SolutionFigure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20cm and area of ccross section 0.20cm2 . The junction is maintained at a constant temperature 40∘C and the two ends are maintained at 80^(@)C.Calca––tetheamountofheattakenoutomthecoldjunction∈o≠minuteafterthesteadystateisreached.TheconductivitiesareK_(Al)=200Wm^(-1)^(∘)C−1 . and KCu=400Wm−1^(@)C^(-1) .

View Solution
