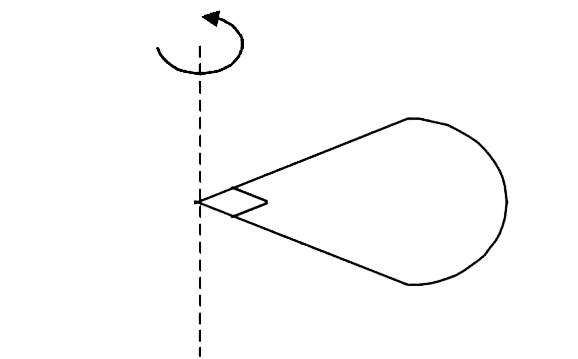
An arm making an angle of $120^{\circ}$ at the center of ring of mass m and radius r is cut from the ring. The arc is made to rotate about z-axis perpendicular to its plane and passing through the center of the ring. The moment of inertia of the arc about the z-axis is

A

$m r^{2}$

B

$\frac{m r^{2}}{3}$

C

$\frac{m r^{2}}{2}$

D

$(m \frac{r^{2}}{4}$

Video Solution

Text Solution

Verified by Experts

b) The mass of ring of per unit angle is $λ = \frac{m}{2 π}$
$∴$ dm-= (m)/(2pi) dtheta $< b r >$ therefore $T h e m o m e n t o f \in e r t i a o f c o n s r e d e \leq m e n t a b o u t z - a ξ s p a s sin g t h r o u g h p \oint O i s < b r > d l =$ r^(2)dm $< b r >$ therefore $t h e m o m e n t o f \in e r t i a o f t h e a r c i s < b r >$ I = r^(2) = (mr^(2)/3 int_(theta=0)^(theta=(2pi//3))) $d m =$ (mr^(2)/3)

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A wire of mass $m$ and length $l$ is bent in the form of circular ring. The moment of inertia of the ring about its axis is
A $\frac{M l}{4 π^{2}}$
B $\frac{M l}{2 π}$
C $\frac{M l}{4 π}$
D $\frac{M l^{2}}{4 π^{2}}$
Question 2 - Select One
One quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. it is made to rotate about a line perpendicular to its plane and passing through the center of the original disc. Its moment of inertia about the axis of rotation is

A $\frac{1}{2} M R^{2}$
B $\frac{1}{4} M R^{2}$
C $\frac{1}{8} M R^{2}$
D $\sqrt{2} M R^{2}$
Question 3 - Select One
There is a ring or mass m and radius R is pivoted at a point O on its periphery. It is free to rotate about an axis perpendicular to its plane. What is the period of ring?
A $T = 2 π ((\frac{R}{g}))$
B $T = 2 π \sqrt{(\frac{2 R}{g})}$
C $T = π \sqrt{(\frac{2 R}{g})}$
D $T = 2 π \sqrt{(\frac{3 R}{g})}$

BITSAT GUIDE-ROTATIONAL MOTION-BITSAT Archives

Home
Ask Doubt
Profile