An athlete swims the length of 50m pool in 20s and makes the return trip to the starting position in 22s, Determine his averge velocity in
a. The first half of the swim
b. The second half of the swim
c. The round trip.
a. vav1=5020=2.5ms−1,
b. vav2=5022=2.27ms−1
c. vav is zero for round trip because displacement is zero.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.2
12 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.3
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A boy swims in a 100 m long pool. He covers 60 m with a velocity of 20 m/s and covers the rest of the distance with a velocity of 10 m/s. Calculate the average velocity of the boy.
View SolutionThe position of an object moving on a straight line is defined by the relation x=t3−2t2−4t, where x is expressed in meter and t in second. Determine
(a) the average velocity during the interval of 1 second to 4 second.
(b) the velocity at t = 1 s and t = 4 s,
(c) the average acceleration during the interval of 1 second to 4 second.
(d) the acceleration at t = 4 s and t = 1 s.
View Solution
Knowledge Check
Anneke is completing in a 500-meter freestyle swim event, which consists of swimming the length of a pool 20 times. If Anneke averages 26.4 seconds per length of the pool. Which of the following equations could be used to determine the number of meter(m) Anneke has left in the event after swimming for s seconds?
Am=500−25s26.4Bm=500−25sCm=25s26.4Dm=500−20sA man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2s). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is 15 m at t = 2. The gap is found to remain constant. The velocities with which the balls were thrown are (Take g = 10ms−1)
A20ms−1,10ms−1B10ms−1,5ms−1C16ms−1,8ms−1D30ms−1,15ms−1
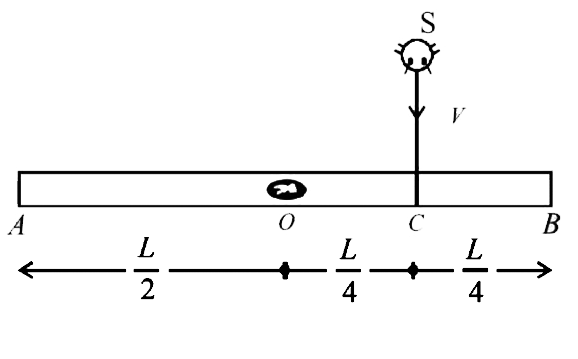
A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
View SolutionSTATEMENT - 1 : Distance is a vector quantity and displacement is a scalar quantity.
STATEMENT - 2 : A person makes a round - trip journey, finishing where she started. The displacement for the trip is 0 and the distance is some nonzero value.
STATEMENT - 3 : A person starts at position A and finishes at position B. The distance for the trip is the length of the segment measured from A to B.
View SolutionA person can swim in still water at 5 m/s. He moves in a river of velocity 3 m/s. First down the stream next same distance up the steam the ratio of times taken are
View SolutionA train starts from rest and moves with a constant accelerationof 2.0ms2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find a. the total distance moved by the train, b. the maximum speed attained by the train and c. the position(s) of the train at half the maximum speed.
View SolutionA man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
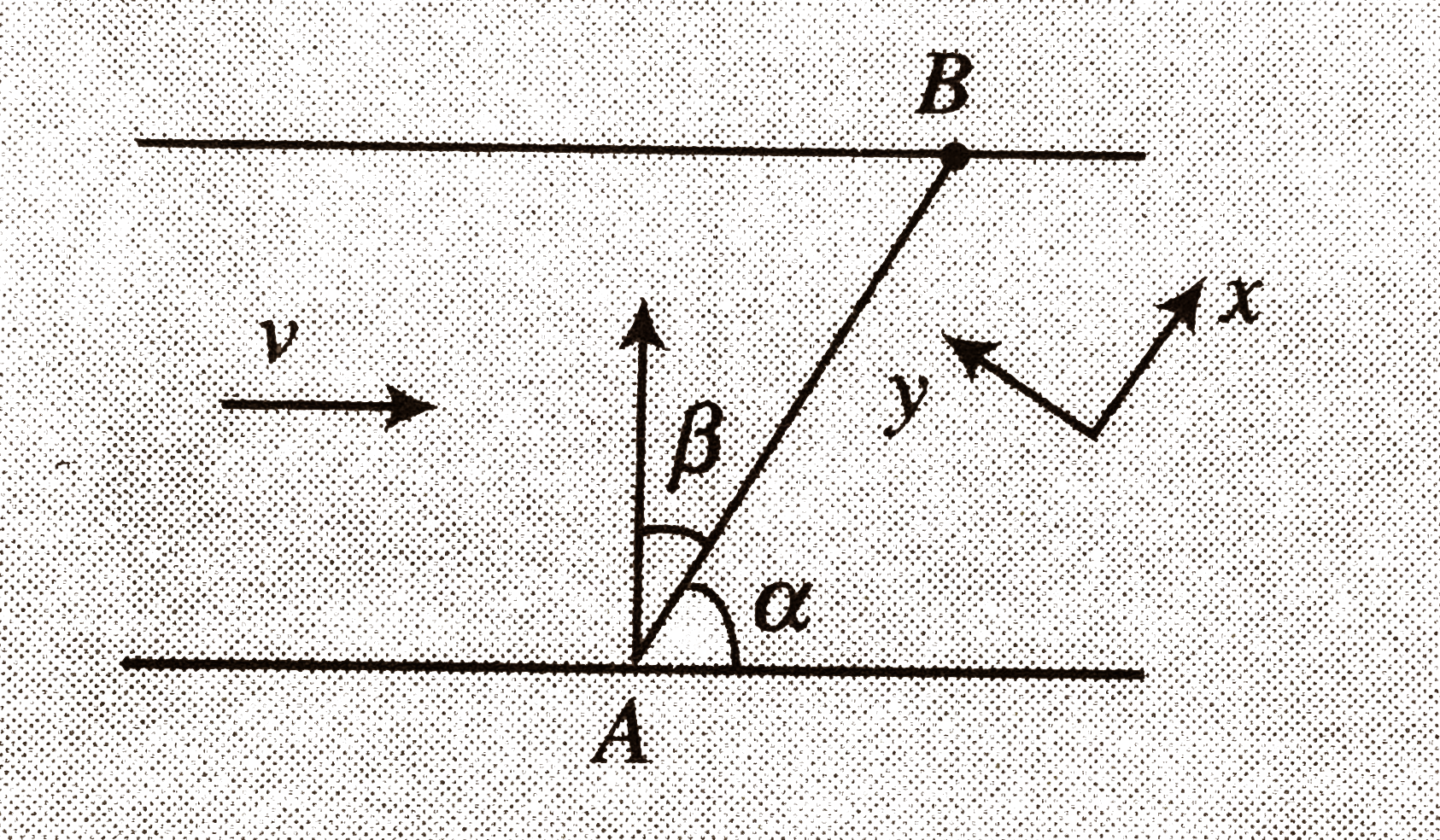 .
.
View SolutionTwo friends A and B (each weighing 40kg) are sitting on a frictionless platform some distance d apart. A rolls a ball of mass 4kg on the platform towards B which B catches. Then B rolls the ball towards A and A catches it. The ball keeps on moving back and forth between A and B. The ball has a fixed speed of 5m/s on the platform.
a. Find the speed of A after he rolls the ball for the first time.
b. Find the speed of A after he catches the ball for the first time.
c. Find the speed of A and B after the ball has made five round trips and is held by A.
d. How many times can A roll the ball?
e. Where is the centre of mass of the system A+B+ ball at. the end of the nth trip?
View Solution
