A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
(i) 12V7L, (ii) 35ms−1

Let us take rod insect as a system. There is not external impulse acting on the system. Hence, we can apply conservation of angular momentum just before and just after collision about the point O. Angular momentum of the system before collision = angular momentum of the system after collision.
MV×L4=Iω
Where I is the moment of inertia of the system just after collision and ω is the angular velocity just after collision.
⇒MV×L4=[M(L4)2+112ML2]ω
⇒MV×L4=ML24[14+13]ω=ML24[3+412]ω=ML24×712×ω⇒ω=127×VL.
Initially the rod was in equilibrium. But after collision there is an extra mass M of the insect which creates a torque in the clockwise direction, which tries to create angular acceleration in the rod. But the same is compensated by the movement of insect towards B due to which moment of inertia of the system increase.
Let at any instant of time t the insect be at a distance x from the centre of the rod and the rod has turned through an angle θ(=ωt) w.r.t. its original position

Torque acting on rod τ=dLdt=ddt(Iω)=ωdIdt
=ωddt[112MI2+Mx2]=2Mω×dxdt.......(i)
This torque is balanced by the torque due to weight of insect τ= Force × Perpendicular distance of force with axis of rotation.
=Mg×(OM)=Mg×xcosθ...........(ii)
From (i) and (ii)
2Mω×dxdt=Mg×xcosθ⇒dx=(g2ω)cosωtdt
On integration taking limits
∫L/2L/4dx+g2ω2∫π/2ω0cosωtdt [when x=L4,ωt=0, when x=L2,ωt=π2]
[x]L/4L/2=g2ω2[sinωt]π/2ω0
⇒L2−L4=g2ω2[sinπ2−sin0]⇒L4=g2ω2⇒ω=√2gL
But ω=127VL⇒127VL=√2gL⇒V=712√2gL⇒V=712√2×10×1.8=3.5ms−1
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (NUMERICAL VALUE TYPE)
15 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
A copper rod AB-of length / pivoted at one end A, rotates at constant angular velocity ω, at right angles to a uniformn magnetic field of induction B. The emf, developed between the mid point of the rod and end B is
View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View Solution
A uniform rod AB of length L and mass m is suspended freely at A and hangs vertically at rest when a particle of same mass m is fired horizontally with speed v to strike the rod at its mid point. If the particle is brought to rest after the impact. Then the impulsive reaction at A is horizontal direction is
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA rod of mass m and length L is pivoted at a point O and kept in horizontal position as shown in figure. Now it is released from this position so that it can rotates freely about the point O in downward direction. When it becomes vertical
View SolutionA rod AC of length l and mass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of same mass m moving on the plane with velocity v strikes the rod at point B making angle 37∘ with the rod. The collision is elastic. After collision,

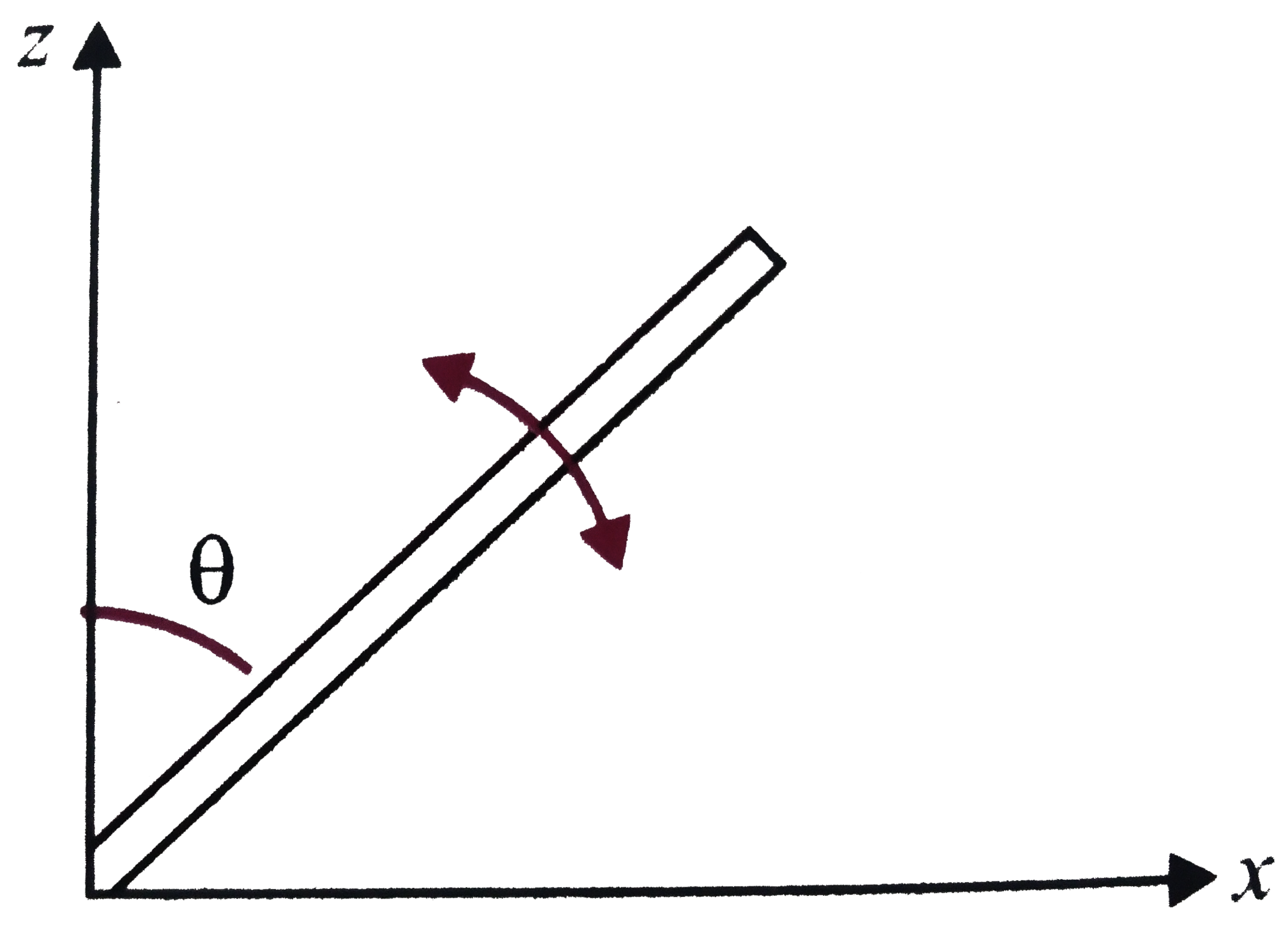
View SolutionA slender uniform rod of mass M and length l is pivoted at one end so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
View SolutionA particle of mass m is fixed to one end of a light rigid rod of length l and rotated in a vertical ciorcular path about its other end. The minimum speed of the particle at its highest point must be
View SolutionA uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at ann angle θ with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?
View Solution
