An effective tactic in tennis, when your opponent is near the net, consists of lofting the ball over his head, forcing him to move quickly away from the net (see figure). Suppose that you loft the ball with an initial speed of 15.0 m/s, at an angle of 50.0∘ above the horizontal. At this instant your opponent is 10.0 m away from the ball. He begins moving away from you 0.30 s later, hoping to reach the ball and hit it back at the moment that it is 2.10 m above its launch point. With what minimum average speed must he move? (Ignore the fact that he can stretch, so that his racket can reach the ball before he does.)
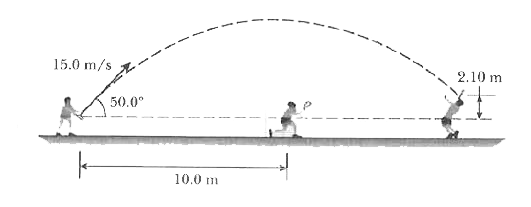
4.98 m/s
5.79 m/s
5.14 m/s
9.64 m/s
The correct Answer is:B
Step by step video, text & image solution for An effective tactic in tennis, when your opponent is near the net, consists of lofting the ball over his head, forcing him to move quickly away from the net (see figure). Suppose that you loft the ball with an initial speed of 15.0 m/s, at an angle of 50.0^(@) above the horizontal. At this instant your opponent is 10.0 m away from the ball. He begins moving away from you 0.30 s later, hoping to reach the ball and hit it back at the moment that it is 2.10 m above its launch point. With what minimum average speed must he move? (Ignore the fact that he can stretch, so that his racket can reach the ball before he does.) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)14videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
A ball is thrown from a field with a speed of 12.0 m/s at an angle of 450 with the horizontal. At what distance will it hit the field again ? Take g=10.0ms2
View SolutionA ball is projected with initial speed u at an angle θ above the horizontal . Calculate the time after which ball will be moving at right angle to its initial velocity.
View Solution
Knowledge Check
- Question 1 - Select One
A baseball is hit into the air at an initial speed of 36.6 m/s and an angle of 50.0∘ above the horizontal. At the same time, the center fielder starts running away from the batter, and he catches the ball 0.914 m above the level at which it was hit. If the center fielder is initially 1.10×102m from home plate, what must be his average speed?
A3.5 m/sB5.0 m/sC4.2 m/sD6.9 m/s - Question 2 - Select One
A boy playing on the roof of a 10m high building throws a ball with a speed of 10m/s at an angle of 30(∘) with the horizontal. How far from the throwing point will the ball be at the height of 10m from the ground ?
[g=10m/s2,sin30∘=12,cos30∘=√32]A5.2mB4.33mC2.66mD8.66m - Question 3 - Select One
A ball is projected horizontal from the top of a tower with a velocity v0. It will be moving at an angle of 60∘ with the horizontal after time.
Av0√3gB√3v0gCv0gDv0g
A soccer ball is kicked from the ground with an initial speed of 21.3 m/s at an upward angle of 45∘. A player 55 m away in the direction of the kick starts running to meet the ball at that instant. What must be his average speed if he is to meet the ball just before it hits the ground?
View SolutionIf the mirror moves away from the object with speed v units, then find the speed of the image that moves away from the object.
View SolutionYou throw a ball toward a wall at speed 25.0 m/s and at angle θ0=40.0∘ above the horizontal. The wall is distance d = 22.0 m from the release point of the ball. (a) How far above the release point does the ball hit the wall? What are the (b) horizontal and ( c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory?
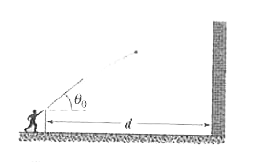 View Solution
View SolutionA ball is fired from point P, with an initial speed of 50ms−1 at an angle of 53∘, with the horizontal. At the same time, a long wall ABat200m from point P starts moving toward P with a constant speed of 10ms−1. Find
(a) the time when the ball collides with wall AB.
(b) the coordinate of point C, where the ball xollides, taking point P as origin.
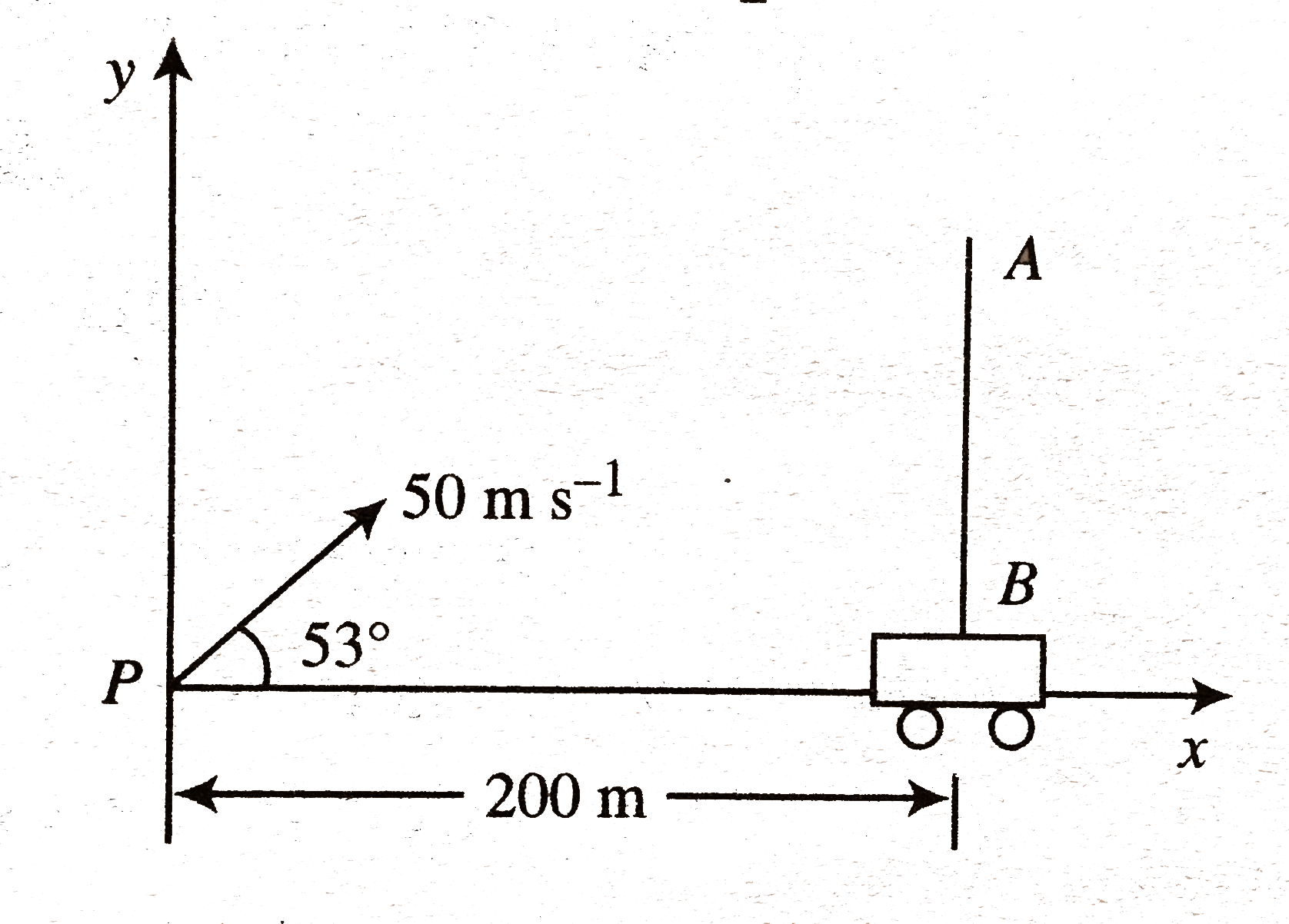 .View Solution
.View SolutionA ball is projected from a point on the floor wilth a speed of 15 m/s at an angle of 600 with the horizontal. Will ilt hit a vertical wall 5 m away from the point of projection and perpendiculaer to the plane of projection without and perpendicular to the plane of projection without hitting the floor? will the answer differ if the wall is 22 m away?
View Solution

