A ball is projected with initial speed u at an angle $θ$ above the horizontal . Calculate the time after which ball will be moving at right angle to its initial velocity.

Text Solution

Verified by Experts

Let particle be projected from the point A and its velocity become perpendicular to its initial velocity at point B as shown in the figure . Let velocity of the ball at point B be v . Refer to the figure to understand that velocity at point B will make an angle $θ$ with the vertical.

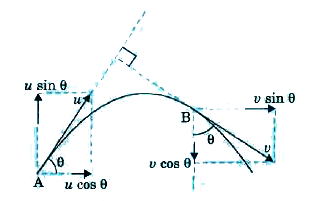
Components of velocities are shown in figure . We know that horizontal component of velocity remains constant, hence we can write the following:
$v sin θ = u cos θ$
$\Rightarrow v = \frac{u cos θ}{sin θ}$
Let us asume upward direction as positive direction and apply equation of kinematics .
$v_{y} = u_{y} + a_{y} t$
$\Rightarrow (- v cos θ) = (u sin θ) + (- g) t$
Substituting value of v from equation (i), we get the following:
$gt = u sin θ + \frac{u cos θ}{sin θ} cos θ$
$t = \frac{u}{g} cos e c θ$

Updated on:21/07/2023

A particle is projected with initial velocity u making an angle $α$ with the horizontal, its time of flight will be given by
A $\frac{2 u sin α}{g}$
B $\frac{2 u^{2} sin α}{g}$
C $\frac{u sin α}{g}$
D $\frac{u^{2} sin α}{g}$
A particle is projected from a point P with a velocity v at an angle $θ$ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
AVelocity of particle at Q is $v sin θ$
BVelocity of particle at Q is $v cot θ$
CTime of flight from P to Q is $(v / g) cos e c θ$
DTime of flight from P to Q is $(v / g) sec θ$
A particle is project d from point A with velocity u at an angle $α$ with horizontal. In its parabolic path, at point P the particle is moving at right angles to its initial direction of projection. Its velocity at P is:
A $u tan α$
B $u cot α$
C $u cos α$
D $u cos e c α$