An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because,
the two magnetic forces are equal and opposite, so they produce no net effect
the magnetic forces do not work on each particle
the magnetic forces do equal and opposite (butnon-zero) work on each particle
the magnetic forces are necessarily negligible
The correct Answer is:B
To solve the question, we need to understand the interaction between the electron and proton and the role of magnetic forces in their motion.
1. Understanding the Forces:
- An electron and a proton are charged particles. When they move, they create electric and magnetic fields. The electric force between them is attractive due to their opposite charges.
2. Magnetic Forces:
- As the electron and proton move, they also exert magnetic forces on each other. However, these magnetic forces act perpendicular to the direction of their motion.
3. Work Done by Forces:
- Work is defined as the force applied on an object times the displacement of that object in the direction of the force. Mathematically, W=F⋅d⋅cos(θ), where θ is the angle between the force and the displacement.
- Since the magnetic force is perpendicular to the motion of the particles, the angle θ is 90 degrees. Therefore, cos(90∘)=0. This means that the magnetic force does no work on the particles.
4. Conclusion:
- Because the magnetic forces do not do any work on the electron and proton, they do not contribute to the change in kinetic energy of the system. Thus, when calculating the change in kinetic energy, we can ignore the magnetic forces.
5. Final Answer:
- The correct reason for ignoring the magnetic force in the calculation of kinetic energy change is that magnetic forces do not work on each particle.
- An electron and a proton are charged particles. When they move, they create electric and magnetic fields. The electric force between them is attractive due to their opposite charges.
- As the electron and proton move, they also exert magnetic forces on each other. However, these magnetic forces act perpendicular to the direction of their motion.
- Work is defined as the force applied on an object times the displacement of that object in the direction of the force. Mathematically, W=F⋅d⋅cos(θ), where θ is the angle between the force and the displacement.
- Since the magnetic force is perpendicular to the motion of the particles, the angle θ is 90 degrees. Therefore, cos(90∘)=0. This means that the magnetic force does no work on the particles.
- Because the magnetic forces do not do any work on the electron and proton, they do not contribute to the change in kinetic energy of the system. Thus, when calculating the change in kinetic energy, we can ignore the magnetic forces.
- The correct reason for ignoring the magnetic force in the calculation of kinetic energy change is that magnetic forces do not work on each particle.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRANCE SPECIAL QUESTIONS
16 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
Assertion: Internal forces cannot change linear momentum.
Reason: Internal forces can change the kinetic energy of a system.
View SolutionA : Internal forces can change the kinetic energy but not the momentum of the system.
R : The net internal force on a system is always zero.
View SolutionA particle is moving under the influence of a force which is fixed in magnitude and acting at an angle θ in the direction of motion. The path described by the particle is
View SolutionThere is no change in the energy of a charged particle moving in a magnetic field although a magnetic force is acting on it . True/False.
View SolutionAn electron and a proton are moving with the same kinetic energy along the same direction, When they pass through a uniform magnetic field perpendicular to the direction of their motion, they describe circular path of the same radius. Is this statement true or false?
View SolutionStatement 1: A charged particle is moving in a circular path under the action of a uniform magnetic field as shown in Fig. During motion kinetic energy of charged particle is costant.
Statement 2: During the motion, magnetic force acting on the particle is perpendicular to instantaneous velocity.

View SolutionA long cylindrical wire carries a positive charge of linear density 2.0 x 10^(-8) C m^(-1). An electron revolves around it in a circular path under the influence of the attractive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
View SolutionA particle moves in one dimension from rest under the influence of a force that varies with the distance travelled by the particle as shown in the figure. The kinetic energy of the particle after it has travelled 3m is:
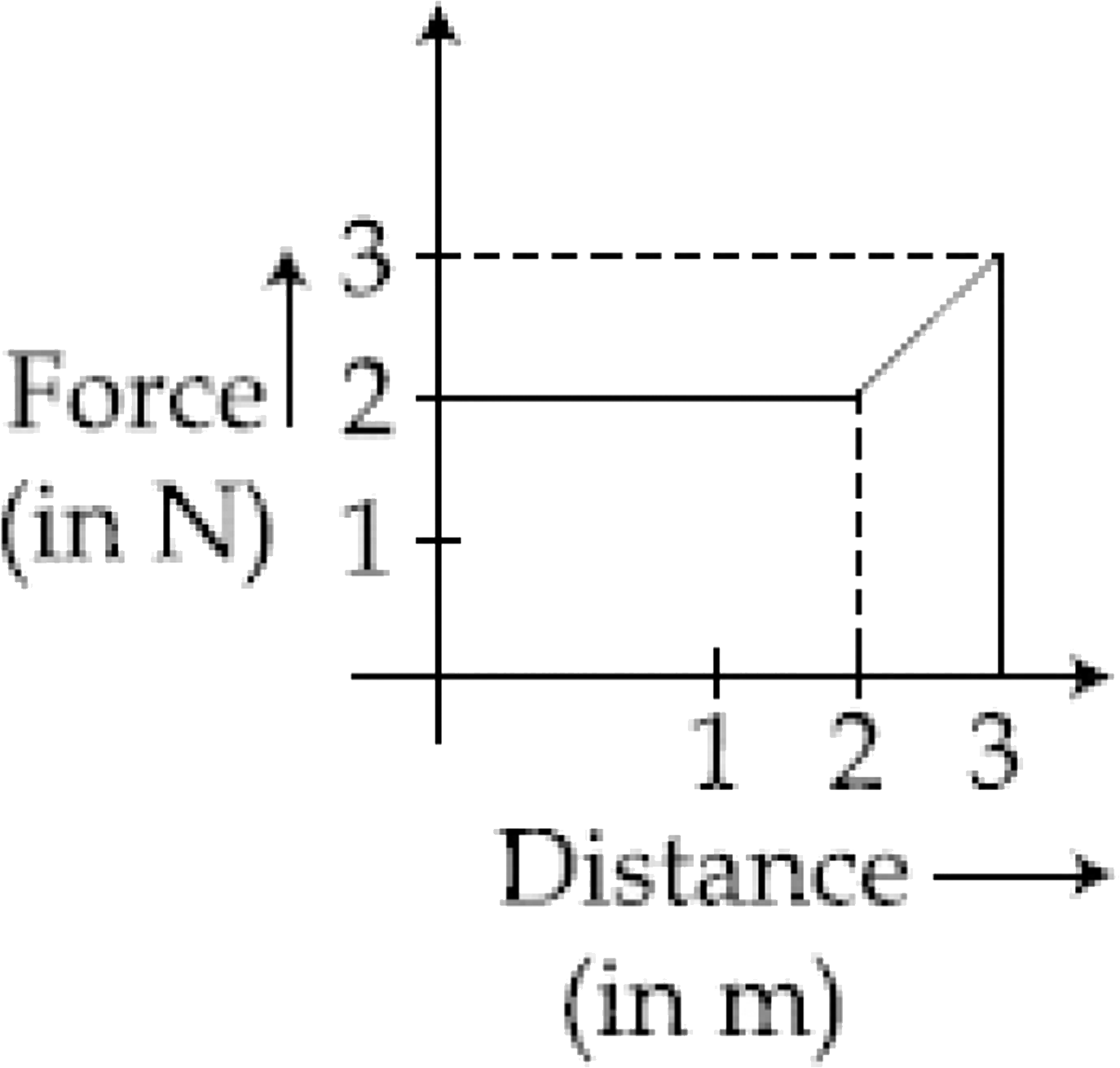
View SolutionFor a particle moving under the action of a variable force, kinetic energy (k) versus position (x) graph is given, then
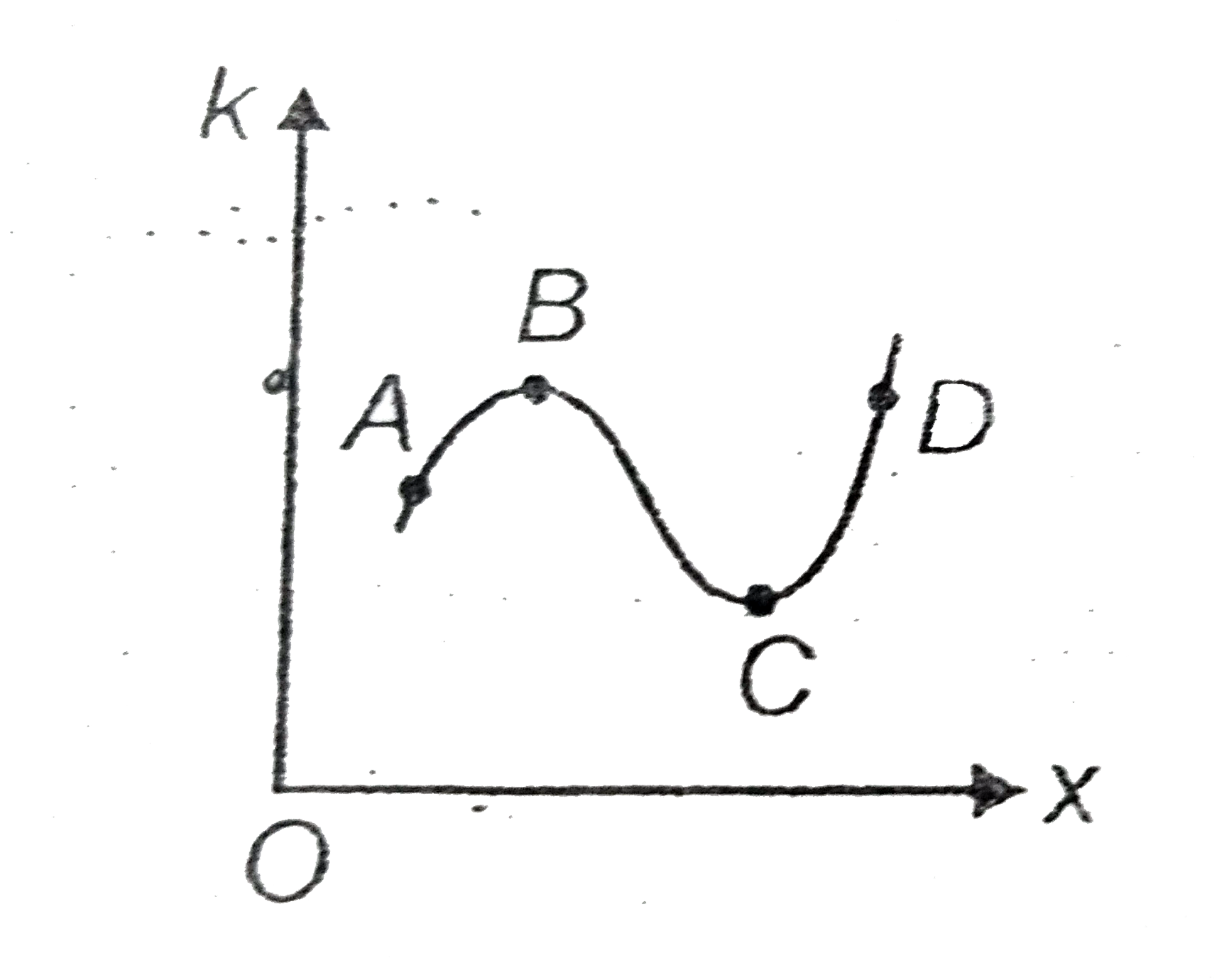
View SolutionFor a particle moving under the action of a variable force, kinetic energy (k) varsus position (x) graph is given, then

View Solution
