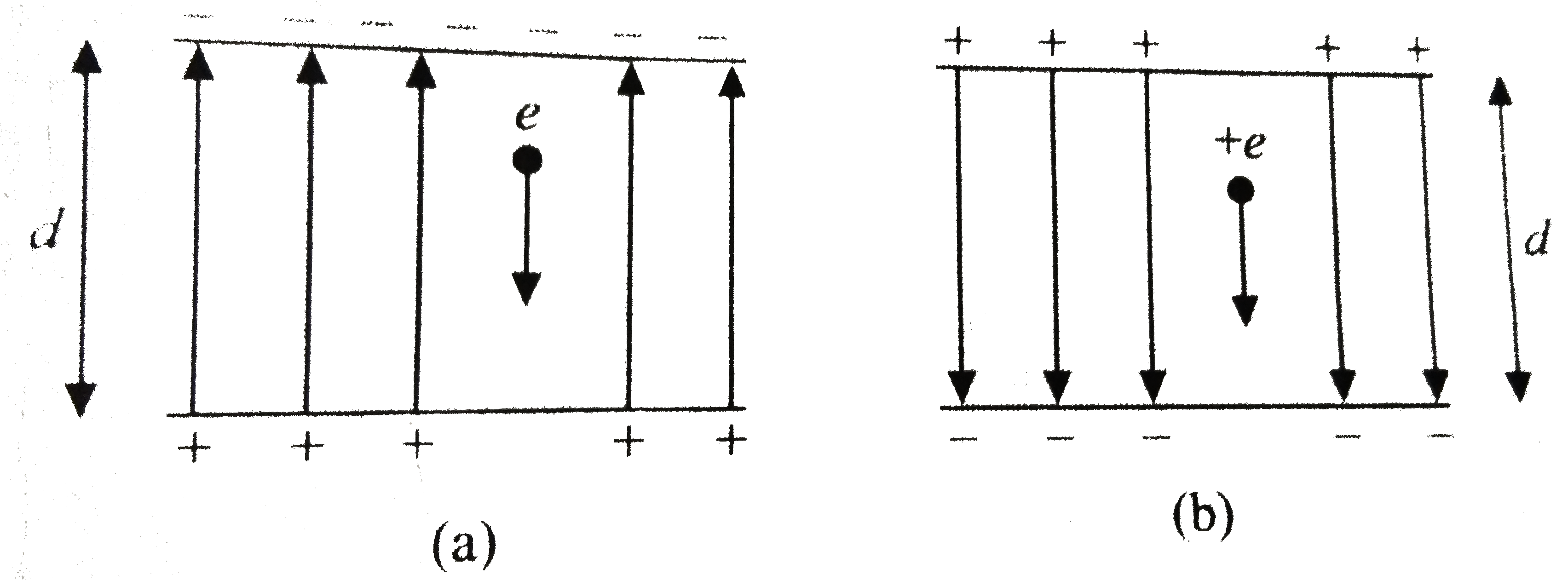
An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
![An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4xx10^(4) NC^(-1) [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/SLA_NP_PHY_XII_C01_S01_034_Q01.png)
Step by step video & image solution for An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4xx10^(4) NC^(-1) [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATIC FORCES, CHARGES AND FIELDSBOOK - SL ARORACHAPTER - ELECTROSTATIC FORCES, CHARGES AND FIELDSEXERCISE - Problems
18 Videos
- ELECTROSTATIC FORCES, CHARGES AND FIELDSBOOK - SL ARORACHAPTER - ELECTROSTATIC FORCES, CHARGES AND FIELDSEXERCISE - Problems For Self Practice
1 Videos
- ELECTRONS AND PHOTONSBOOK - SL ARORACHAPTER - ELECTRONS AND PHOTONSEXERCISE - TYPE E : Problem For Self Practice
11 Videos
- HEATING EFFECT OF CURRENTBOOK - SL ARORACHAPTER - HEATING EFFECT OF CURRENTEXERCISE - All Questions
192 Videos
Similar Questions
An electron falls through a distance of 1.5cm in a uniform electric field of value 2×104N/C, opposite to direction of fall. Compare the time of fall with 'free fall under gravity'.
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View Solution
Knowledge Check
An electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
ASame in both casesBMore in the case of electronCMore in the case of protonDIndependent of chargeAn electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
A1.3×102sB2.1×10−2sC1.6×10−10sD2.9×10−9sAn electron initially at rest falls a distance of 2 cm in a uniform electric field of magnitude 3×104NC−1. The time taken by the electron to fall to this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.75×10−9s
An electron falls through a distance 1.5 cm in a uniform electric field of magnitude 2.0×104NC−1 .Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed keeping its magnitude uncharged , calculate the time taken by a proton to fall through this distance starting from rest.
View SolutionA proton falls dwon through a distance of 2 cm in a uniform electric field of magnitude 3.34×103NC−1. Determine (i) the acceleration of the electron (ii) the time taken by the proton to fall through the distance of 2 cm, and (iii) the direction of the electric field.
View SolutionAn electron moves a distance of 6.0 cm when accelerated from rest by an electric field of strength 2×10−4NC−1. Calculate the time of travel.
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
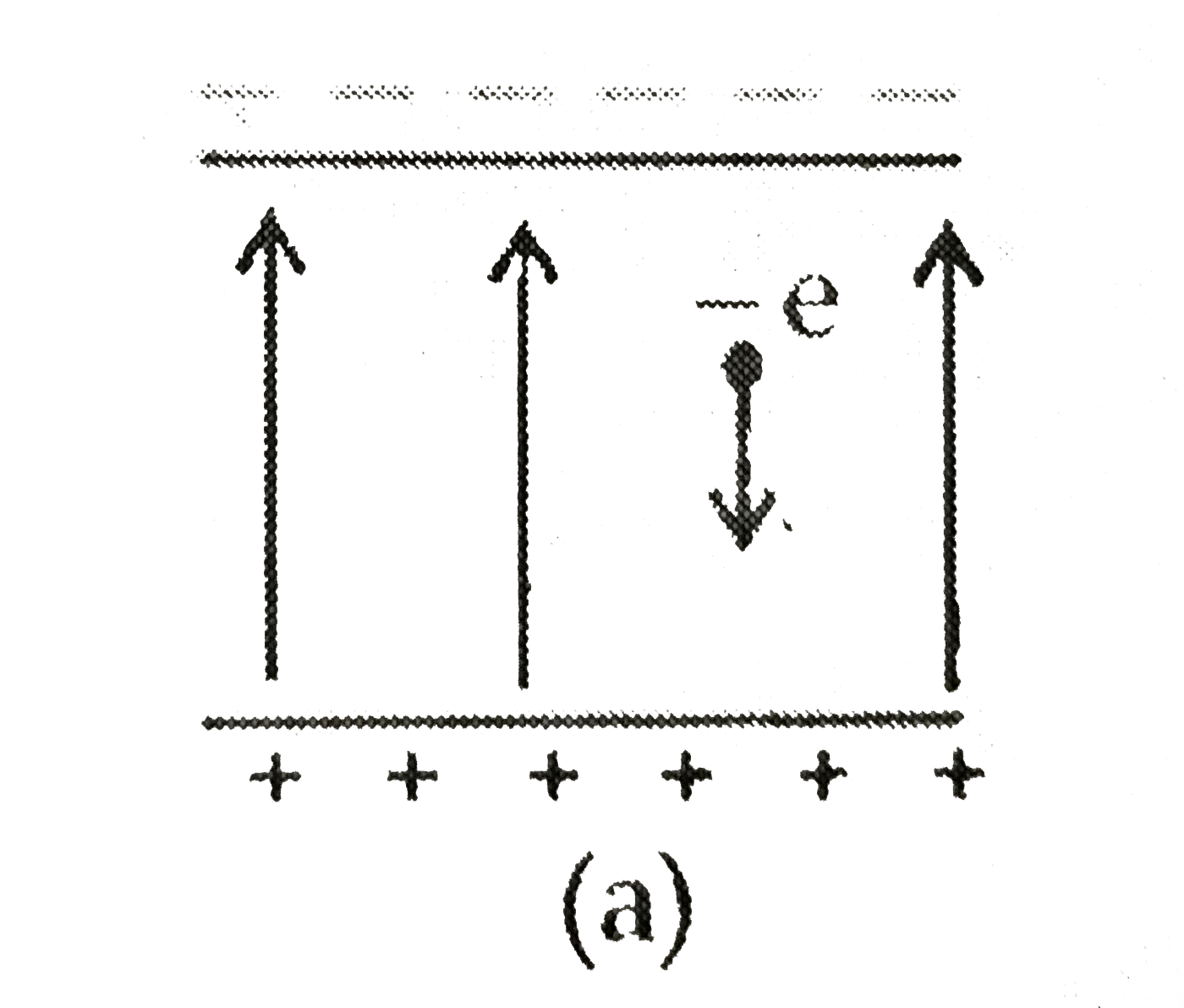
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged, calculate the time taken by a proton to fall through this distance starting from rest.

View SolutionAn electron falls from rest through a vertical distance h in a uniform and vertically upwards directed electric field E. The direction of electric field is now reversed , keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h. The time of fall of the electron, in comparison to the time of fall proton is
View Solution
