An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
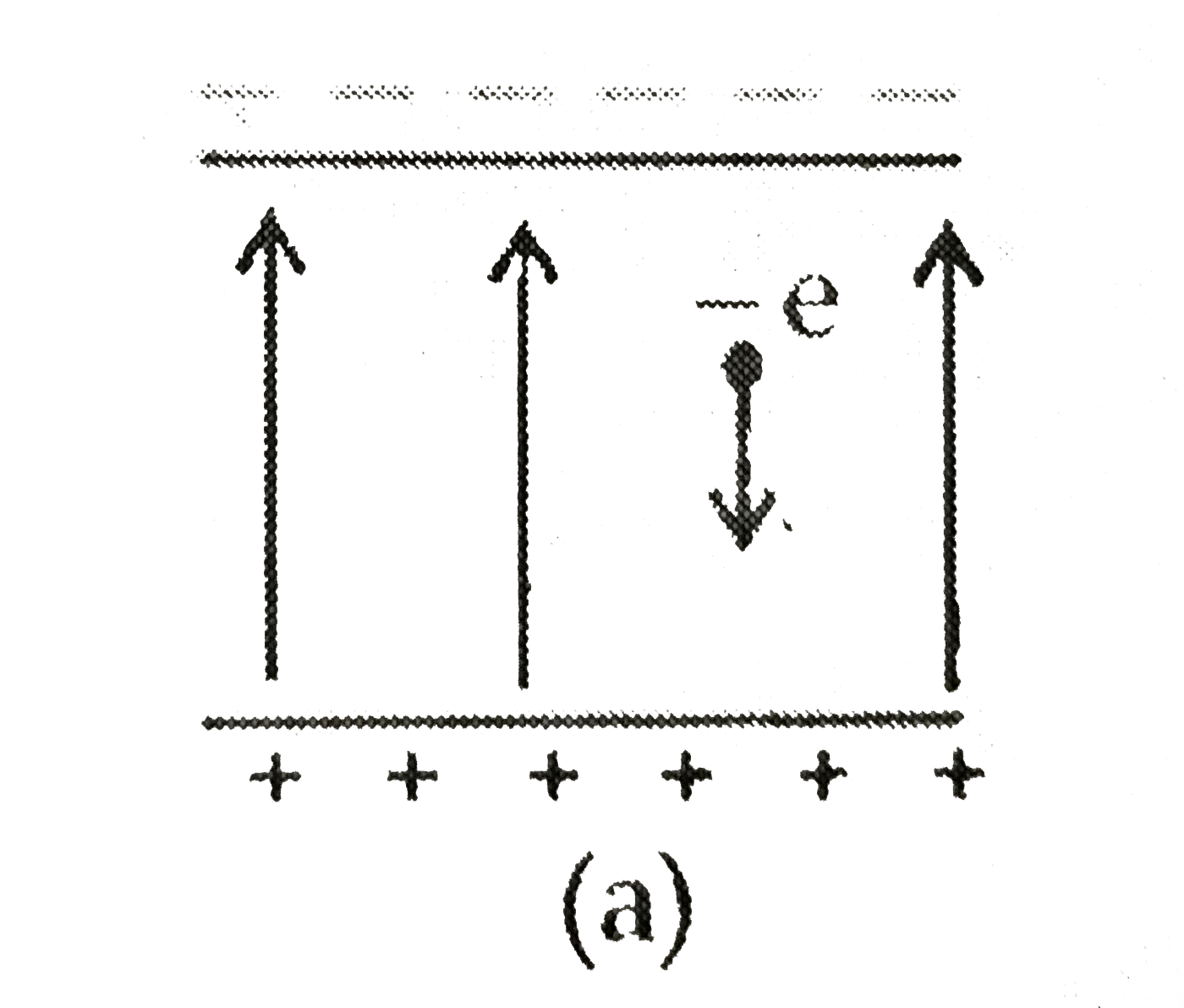
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged, calculate the time taken by a proton to fall through this distance starting from rest.

The field is upward , so the negatively charged particle , electron experiences a downward froce of magnitude eE where E is the magnitude of the electric field.
The acceleration of the electron is ae =eEme
Starting from rest , the time required by the electron to fall through a distance h
te=√2hae=√2hmeeE=√2×1.5×10−2×9.11×10−311.6×10−19×2.0×10−4=2.9×10−9S.
The field is downward , and the positively charged proton experiences a downward force of magnitude eE . The acceleration of the proton is
aP=eEmp
Hence , the time taken by the proton
tp=√2hap=√2hmpeE=√2×1.5×10−2×1.67×10−271.6×10−19×2.0×10−4=1.3×10−7sec.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION - D
6 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION - E
6 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - [SET -III, OUTSIDE DELHI]
5 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
An electron falls through a distance 1.5 cm in a uniform electric field of magnitude 2.0×104NC−1 .Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed keeping its magnitude uncharged , calculate the time taken by a proton to fall through this distance starting from rest.
View SolutionAn electron falls through a distance of 1.5cm in a uniform electric field of value 2×104N/C, opposite to direction of fall. Compare the time of fall with 'free fall under gravity'.
View Solution
Knowledge Check
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
A1.3×102sB2.1×10−2sC1.6×10−10sD2.9×10−9sAn electron initially at rest falls a distance of 2 cm in a uniform electric field of magnitude 3×104NC−1. The time taken by the electron to fall to this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.75×10−9sAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
ASame in both casesBMore in the case of electronCMore in the case of protonDIndependent of charge
A proton falls dwon through a distance of 2 cm in a uniform electric field of magnitude 3.34×103NC−1. Determine (i) the acceleration of the electron (ii) the time taken by the proton to fall through the distance of 2 cm, and (iii) the direction of the electric field.
View SolutionAn electron moves a distance of 6.0 cm when accelerated from rest by an electric field of strength 2×10−4NC−1. Calculate the time of travel.
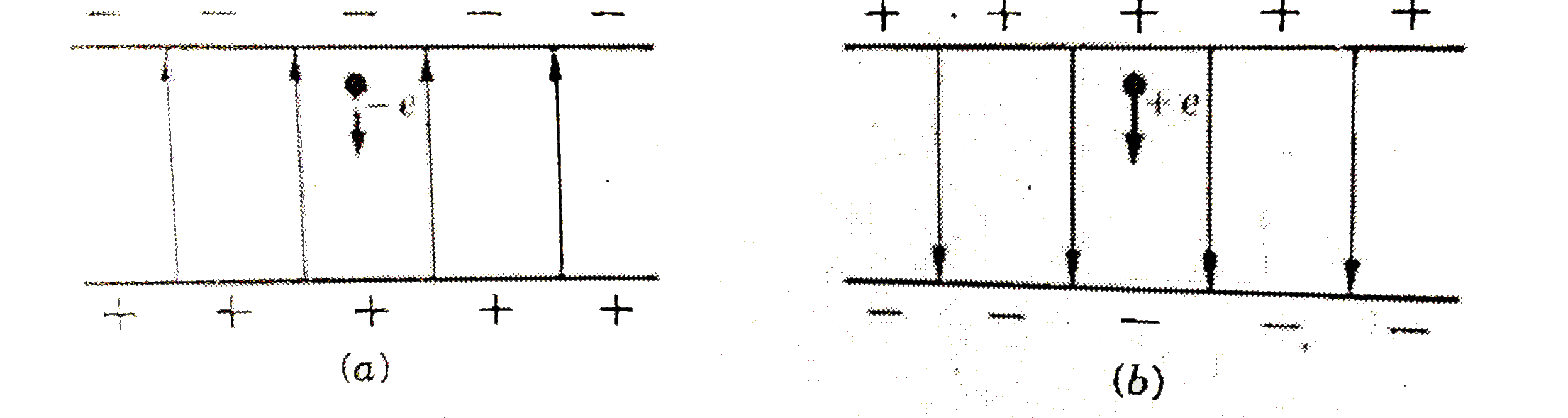
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
View SolutionAn electron is released from rest in a uniform electric field of magnitude 2.00×104N/C . (a) Calculate the acceleration of the electron. (Ignore gravitational) (b) How much time does the electron take to reach 1.00 % of the speed of light ?
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
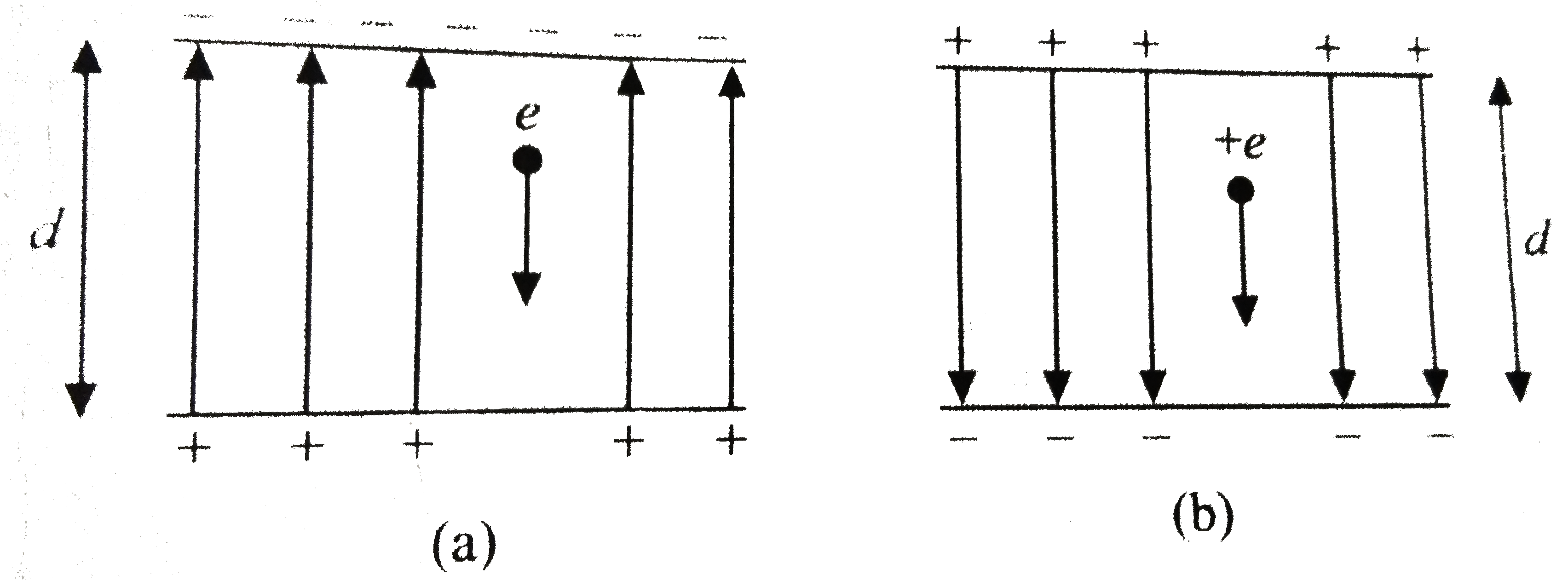 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View Solution
