An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
![An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4xx10^(4) NC^(-1) [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/SLA_NP_PHY_XII_C01_S01_034_Q01.png)
In Fig. 1.13(a) the field is upward, so the negatively charged electron experiences a downward force of magnitude eE where E is the magnitude of the electric field. The acceleration of the electron is
ae=Ee/m
where, me is the mass of the electron
Starting from rest, the time required by the electron to fall through a
distance h is given by
tp=√2hap=√2hmpeE
Fore=1.6×10−19C,me=9.11×10−31kg,
E=2.0×104NC−1,h=1.5×10−2m,
te=2.9×10−9s)
In Fig. 1.13 (b), the field is downward, and the positively charged proton experiences a downward force of magnitude eE. The acceleration of the proton is
ap=eE/mp
where mp is the mass of the proton : mp=1.67×10−27kg. The time of fall for the proton is
tp=√2hap=√2hmpeE=1.3×10−7s
Thus, the heavier particle (proton) takes a greater time to fall through the same distance. This is in basic contrast to the situation of ‘free fall under gravity’ where the time of fall is independent of the mass of the body. Note that in this example we have ignored the acceleration due to gravity in calculating the time of fall. To see if this is justified, let us calculate the acceleration of the proton in the given electric field: ap=eEmp
(1.6×10−19C)×(2.0×104NC−1)1.67×10−27kg
1.9×1012ms−2which is enormous compared to the value of g (9.8 m s–2), the acceleration due to gravity. The acceleration of the electron is even greater. Thus, the effect of acceleration due to gravity can be ignored in this example
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise34videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NCERT ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - All Questions32videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise17videos
ELECTROMAGNETIC INDUCTION
Similar Questions
An electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View Solution
Knowledge Check
- Question 1 - Select One
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.9×10−9s - Question 2 - Select One
A circular plane sheet of radius 10 cm is placed in a uniform electric field of 5×105NC−1, making an angle of 60∘ with the field. Calculate electric flux through the sheet.
A1.36×102Nm2C−1B1.36×104Nm2C−1C0.515×102Nm2C−1D0.515×104Nm2C−1
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
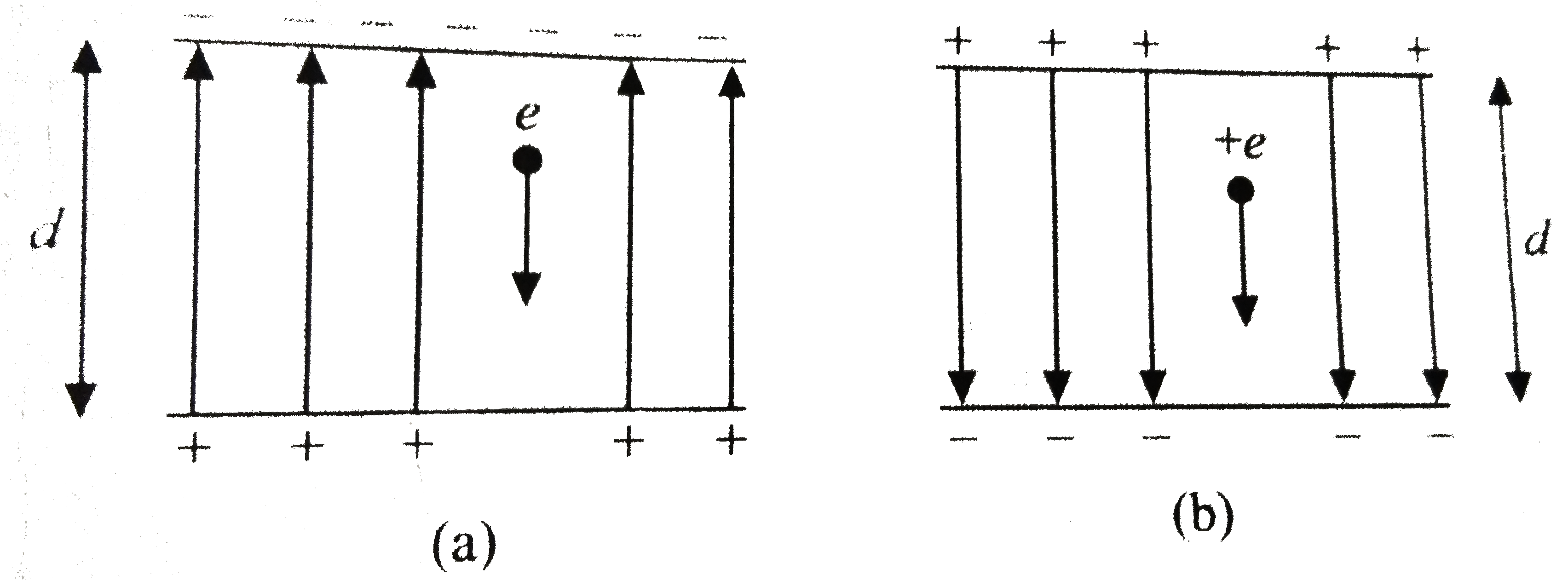 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
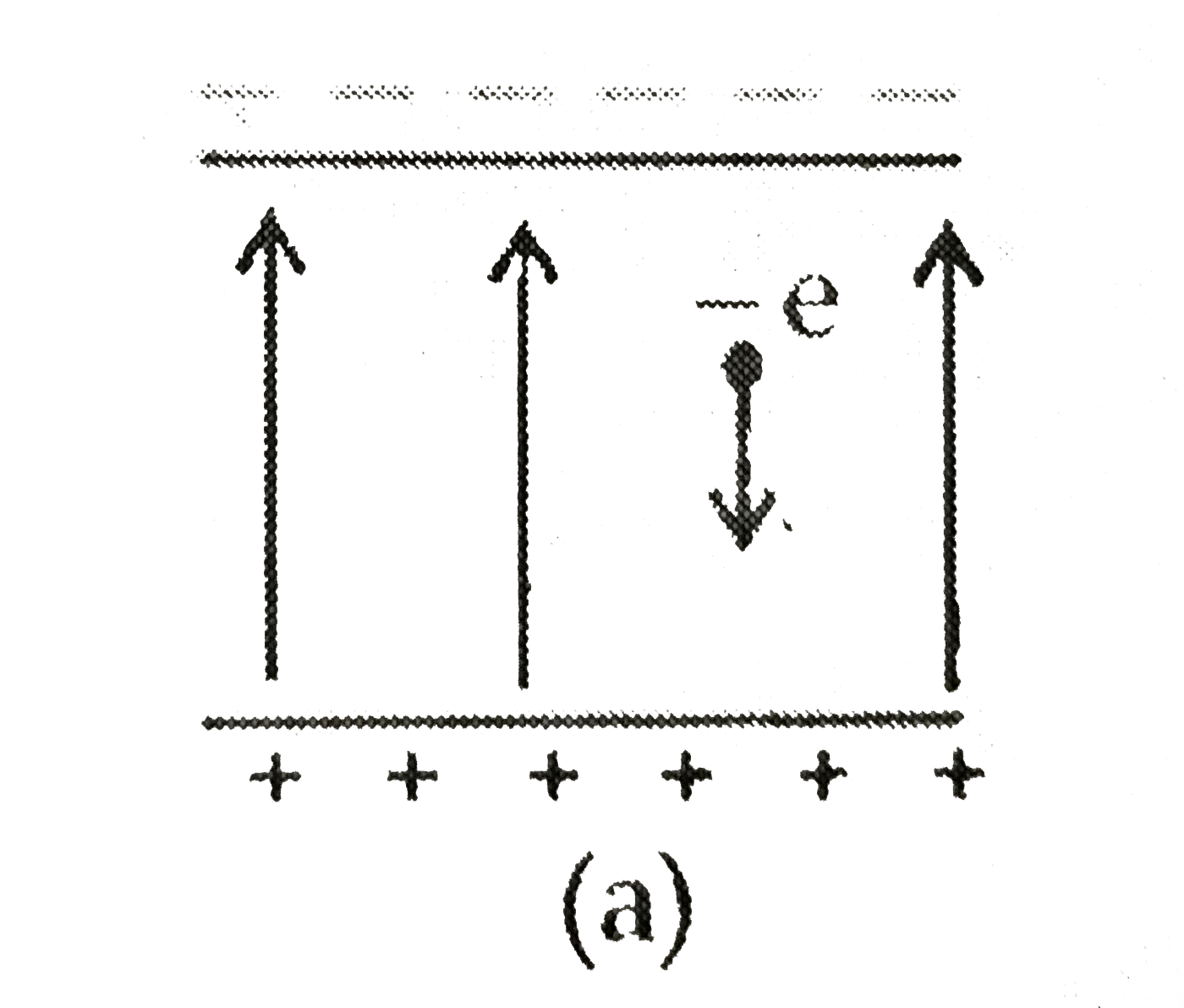
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged , calculate the time taken by a proton to fall through this distance starting from rest.
 View Solution
View SolutionAn electron falls from rest through a vertical distance h in a uniform and vertically upward directed electric field E. the direction of electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h.The time of fall of the electron, in comparison to the time of flal of the proton is
View SolutionAn electrtic dipole with dipole moment 4×10−9Cm is aligned at 30∘ with the direction of a uniform electric field of magnitude 5×104NC−1. Calculate the magnitude of the torque acting on the dipole .
View SolutionAn electron entering field normally with a velocity 4×107ms−1 travels a distance of 0.10 m in an electric field of intensity 3200Vm−1. What is the deviation from its path?
View Solution

