An electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
same in both cases
more in the case of an electron
more in thecase of proton
independent of charge
The correct Answer is:C
To solve the problem, we need to analyze the motion of an electron and a proton falling through the same distance in a uniform electric field. We will derive the time taken for each particle to fall and then compare them.
Step 1: Understand the Forces Acting on the Particles
In an electric field E, a charged particle experiences a force given by:
F=qE
Where q is the charge of the particle. For an electron, q=−e (negative charge) and for a proton, q=+e (positive charge).
Step 2: Calculate the Acceleration of Each Particle
Using Newton's second law, the acceleration a of each particle can be calculated as:
F=ma⟹a=Fm
For the electron:
ae=−eEme
For the proton:
ap=eEmp
Step 3: Set Up the Equation of Motion
We can use the equation of motion for uniformly accelerated motion to find the time taken to fall through a distance h:
h=12at2
Rearranging gives:
t=√2ha
Step 4: Substitute the Accelerations
For the electron:
te=√2hae=
⎷2h−eEme=√−2hmeeE
For the proton:
tp=√2hap=
⎷2heEmp=√2hmpeE
Step 5: Compare the Times
Now we can find the ratio of the time taken by the electron to the time taken by the proton:
tetp=√−2hmeeE√2hmpeE=√memp
Since the mass of the proton mp is much greater than the mass of the electron me, we have:
te<tp
This means the time taken by the proton to fall through the same distance is greater than that of the electron.
Conclusion
The time of fall for the proton will be greater than that of the electron.
---
In an electric field E, a charged particle experiences a force given by:
F=qE
Where q is the charge of the particle. For an electron, q=−e (negative charge) and for a proton, q=+e (positive charge).
Using Newton's second law, the acceleration a of each particle can be calculated as:
F=ma⟹a=Fm
For the electron:
ae=−eEme
For the proton:
ap=eEmp
We can use the equation of motion for uniformly accelerated motion to find the time taken to fall through a distance h:
h=12at2
Rearranging gives:
t=√2ha
For the electron:
te=√2hae=
⎷2h−eEme=√−2hmeeE
For the proton:
tp=√2hap=
⎷2heEmp=√2hmpeE
Now we can find the ratio of the time taken by the electron to the time taken by the proton:
tetp=√−2hmeeE√2hmpeE=√memp
Since the mass of the proton mp is much greater than the mass of the electron me, we have:
te<tp
This means the time taken by the proton to fall through the same distance is greater than that of the electron.
The time of fall for the proton will be greater than that of the electron.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct Answer Type
1 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
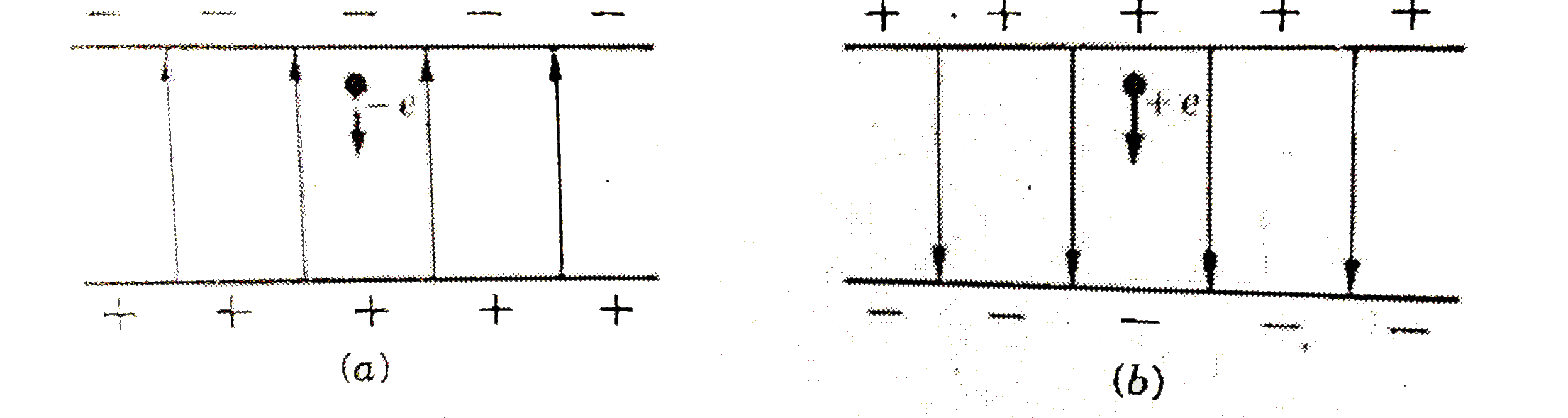
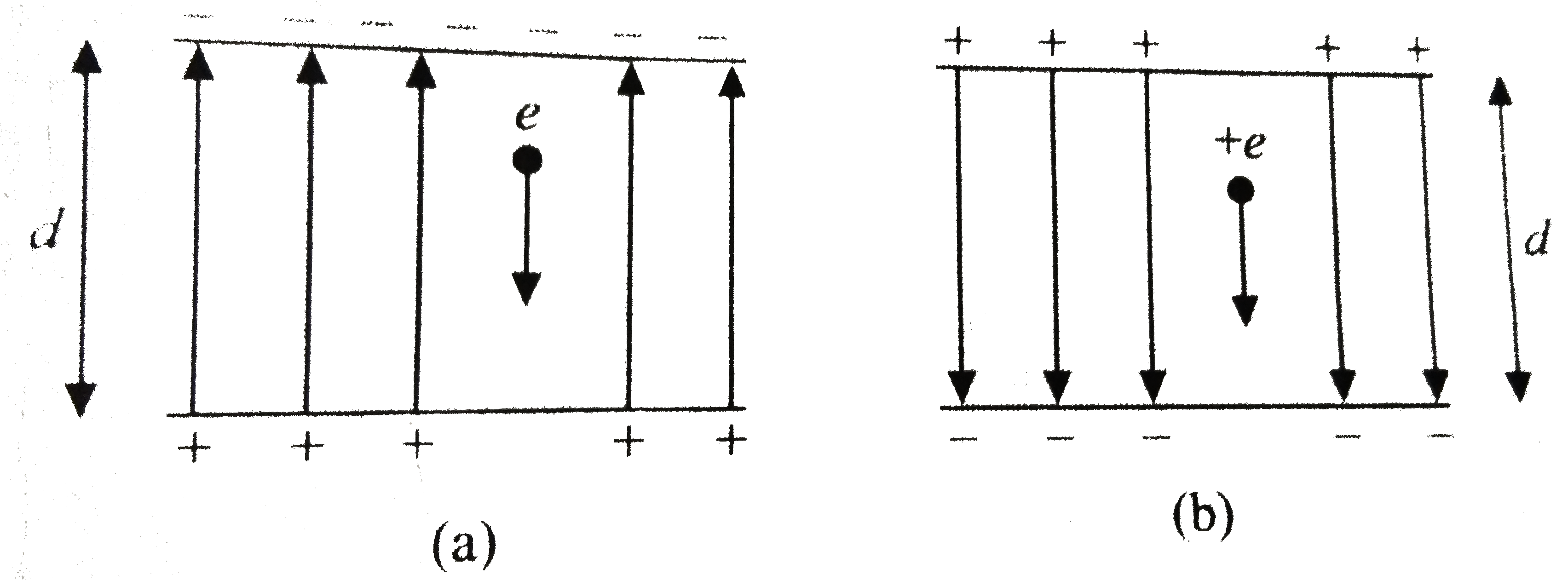
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View Solution
Knowledge Check
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.9×10−9sA circular plane sheet of radius 10 cm is placed in a uniform electric field of 5×105NC−1, making an angle of 60∘ with the field. Calculate electric flux through the sheet.
A1.36×102Nm2C−1B1.36×104Nm2C−1C0.515×102Nm2C−1D0.515×104Nm2C−1
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
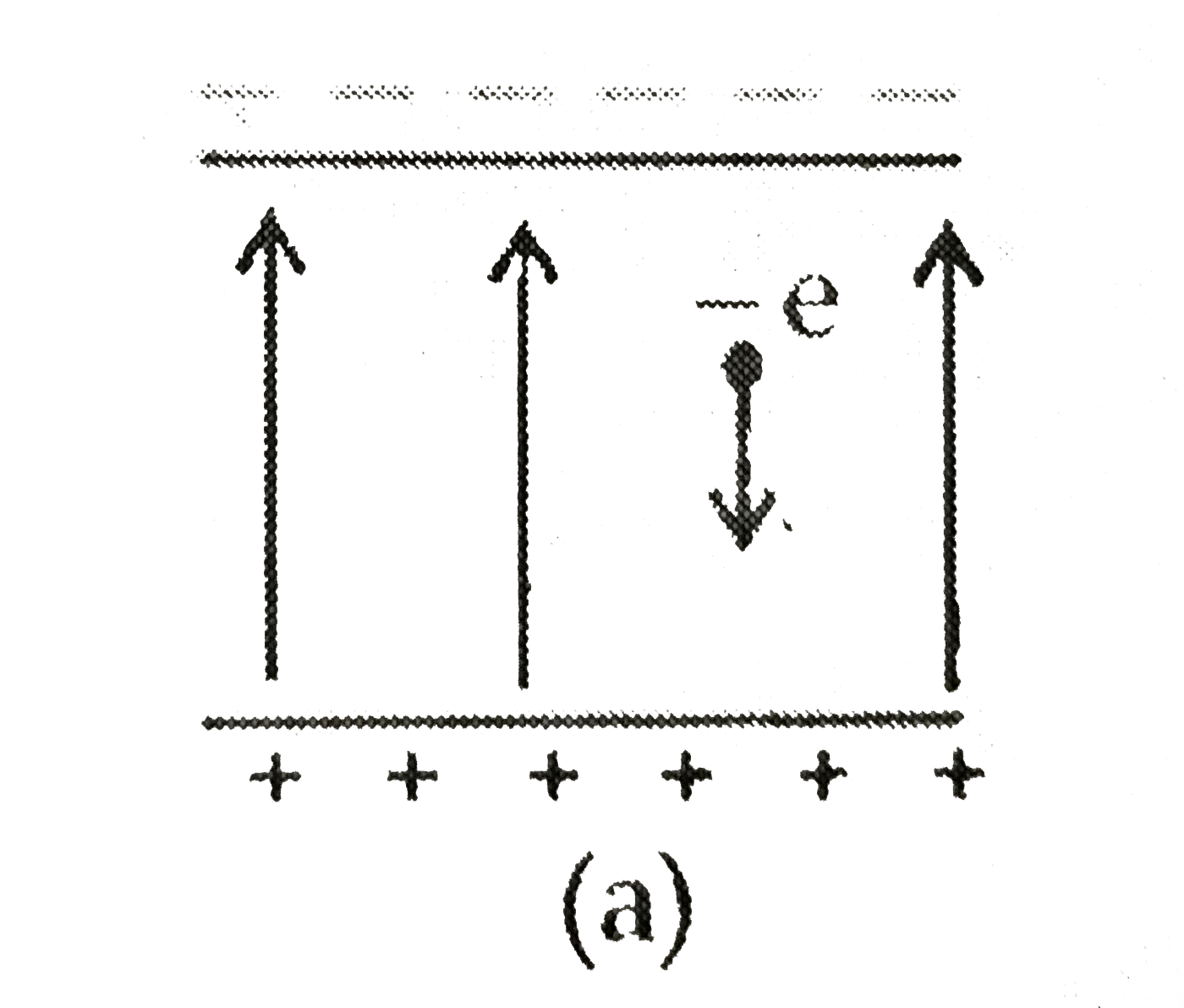
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged , calculate the time taken by a proton to fall through this distance starting from rest.

View SolutionAn electron falls from rest through a vertical distance h in a uniform and vertically upward directed electric field E. the direction of electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h.The time of fall of the electron, in comparison to the time of flal of the proton is
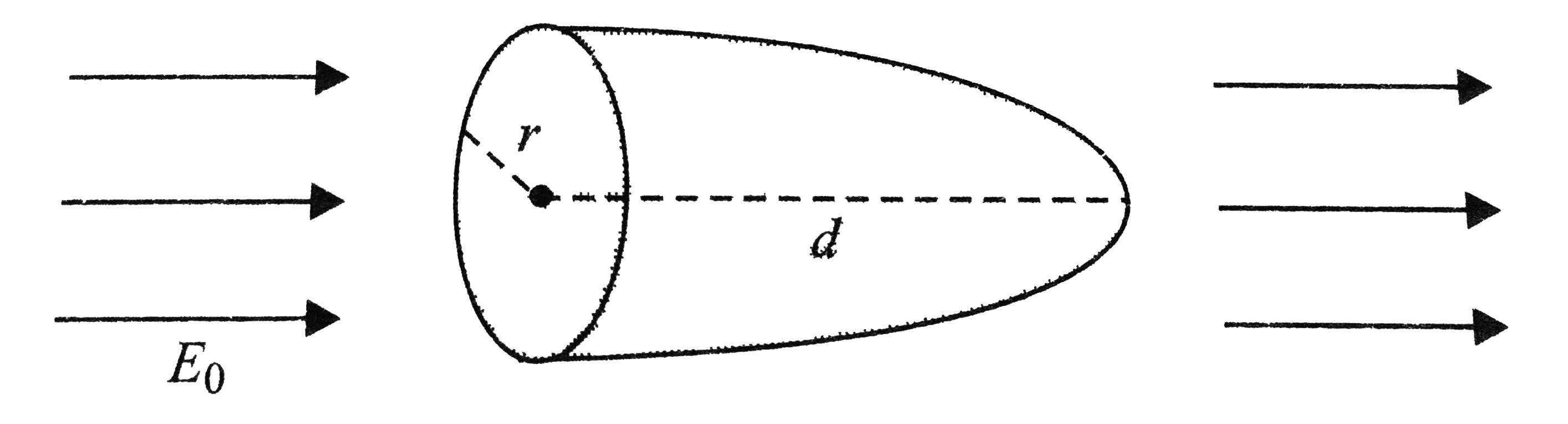
View SolutionCalculate the total electric flux through the paraboloidal surface due to a uniform electric field of magnitude E0 in the direction shown in figure.
View SolutionAn electron accelerated through 500 V , enters a transverse uniform magnetic field of magnitude 100 mT . The radius of the circular path described by the electron is nearly
View SolutionAn electron of mass me initially at rest moves through a certain distance in a uniform electric field in time t1. A proton of mass mp also initially at rest takes time t2 to move through an equal distance in this uniform electric field.Neglecting the effect of gravity, the ratio of t2/t1 is nearly equal to
View Solution
