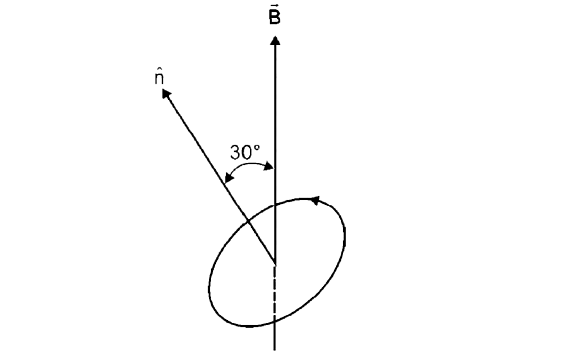
An electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.
The correct Answer is:A, B, C, D
(i) KEY CONCEPT : Orbital magnetic dipole moment M=IA where I is the current due to orbital motion of electron and A is the area of loop made by electron.
rArr M=eT×πR2⇒M=eω2π×πR2
rArr M=12eωR2
But according to Bohr's postulate
mRω2=nh2π⇒Rω2=nh2πm
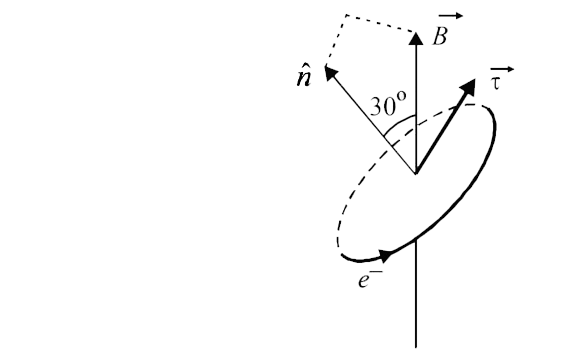
rArr M=e2×nh2πm=nhe4πm=eh4πm (because n=1 for ground state) ltbr> (ii) KEY CONCEPT : We know that torque
→τ=→M×→B⇒τ=MBsinθ
where θ is the angle between MandB
rArr τ=he4πm×Bsin30∘=heB8πm

Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - MCQs(d )
1 Videos
- MODERN PHYSICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer
1 Videos
- RAY AND WAVE OPTICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - RAY AND WAVE OPTICSEXERCISE - JEE Main And Advanced
209 Videos
Similar Questions
An electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.
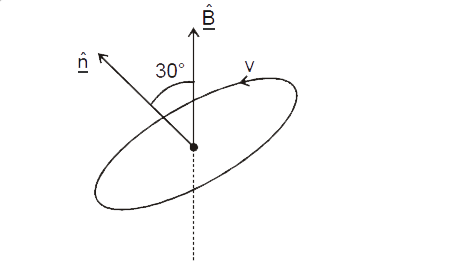
Obtain an expression for the orbital magnetic dipole moment of the electron.
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in a circular orbit of radius R.

(i) The expression for the orbital magnetic moment of the electrton is ehnπm. Find n □
(ii) The atom is placed in a uniform magnetic induction B such that the normal to the plane of electron’s orbit makes an angle of 30∘ with the magnetic induction. The torque experienced by the orbiting electron is ehBnπm. Find n □
View Solution
Knowledge Check
An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
Aeh4πmBeh2πmCeh24πmDe2h4πmMagnetic dipole moment of revolving electron is
AeL2mBe2mCe2MLDemL
An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.
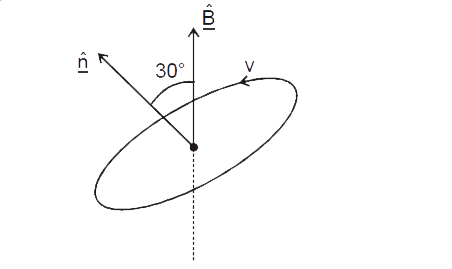
The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.
View SolutionThe minimum magnetic dipole moment of electron in hydrogen atom is
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clock wise direction in a circular orbit. The atom is placed in a magnetic filed such that the normal to the electron orbit makes an angle of 30° with the magnetic field. Find the torque experienced by the orbiting electron.
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.

The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.
View SolutionShow that the orbital magnetic dipole moment of a revolving electron isevr/2.
View Solution
