An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
eh4πm
eh2πm
eh24πm
e2h4πm
The correct Answer is:A
To find the orbital magnetic dipole moment of an electron in the ground state of a hydrogen atom, we can follow these steps:
Step 1: Understand the Concept of Current
The current I due to the revolving electron can be defined as the charge flowing per unit time. For an electron, the charge q is equal to the elementary charge e.
Step 2: Calculate the Time Period
The time period T for one complete revolution of the electron can be calculated using the formula:
T=CircumferenceVelocity=2πRv
where R is the radius of the orbit and v is the velocity of the electron.
Step 3: Find the Velocity Using Bohr's Model
According to Bohr's model, the centripetal force required for the electron to move in a circular orbit is provided by the electrostatic force. The formula is given by:
mv2=ke2R2
where k is Coulomb's constant. Rearranging gives us:
v=√ke2mR
Step 4: Substitute the Velocity into the Time Period Formula
Now we can substitute the expression for v into the time period formula:
T=2πR√ke2mR=2πR√mRke2
Step 5: Calculate the Current
Now we can express the current I:
I=qT=eT=e2πR√mRke2
Step 6: Calculate the Magnetic Dipole Moment
The magnetic dipole moment μ is given by:
μ=I⋅A
where A is the area of the circular orbit:
A=πR2
Substituting the expression for I:
μ=⎛⎜
⎜⎝e2πR√mRke2⎞⎟
⎟⎠⋅πR2
This simplifies to:
μ=eR2√mRke2
Step 7: Final Expression for Magnetic Dipole Moment
After simplifying, we arrive at the final expression for the orbital magnetic dipole moment of the electron in the ground state of the hydrogen atom:
μ=eh4πm
where h is Planck's constant.
Conclusion
Thus, the orbital magnetic dipole moment of the electron in the ground state of a hydrogen atom is given by:
μ=eh4πm
The current I due to the revolving electron can be defined as the charge flowing per unit time. For an electron, the charge q is equal to the elementary charge e.
The time period T for one complete revolution of the electron can be calculated using the formula:
T=CircumferenceVelocity=2πRv
where R is the radius of the orbit and v is the velocity of the electron.
According to Bohr's model, the centripetal force required for the electron to move in a circular orbit is provided by the electrostatic force. The formula is given by:
mv2=ke2R2
where k is Coulomb's constant. Rearranging gives us:
v=√ke2mR
Now we can substitute the expression for v into the time period formula:
T=2πR√ke2mR=2πR√mRke2
Now we can express the current I:
I=qT=eT=e2πR√mRke2
The magnetic dipole moment μ is given by:
μ=I⋅A
where A is the area of the circular orbit:
A=πR2
Substituting the expression for I:
μ=⎛⎜
⎜⎝e2πR√mRke2⎞⎟
⎟⎠⋅πR2
This simplifies to:
μ=eR2√mRke2
After simplifying, we arrive at the final expression for the orbital magnetic dipole moment of the electron in the ground state of the hydrogen atom:
μ=eh4πm
where h is Planck's constant.
Thus, the orbital magnetic dipole moment of the electron in the ground state of a hydrogen atom is given by:
μ=eh4πm
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - ATOMS EXERCISE - The Line Spectra Of Hydrogen Atom6videos
ATOMS
- BOOK - NCERT FINGERTIPSCHAPTER - ATOMS EXERCISE - De Broglie Explanation Of Bohr Model3videos
ATOMS
- BOOK - NCERT FINGERTIPSCHAPTER - ATOMS EXERCISE - Atomic Spectra19videos
ATOMS
- BOOK - NCERT FINGERTIPSCHAPTER - ALTERNATING CURRENT EXERCISE - Assertion And Reason15videos
ALTERNATING CURRENT
- BOOK - NCERT FINGERTIPSCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - HOTS10videos
COMMUNITCATION SYSTEMS
Similar Questions
An electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in a circular orbit of radius R.

(i) The expression for the orbital magnetic moment of the electrton is ehnπm. Find n □
(ii) The atom is placed in a uniform magnetic induction B such that the normal to the plane of electron’s orbit makes an angle of 30∘ with the magnetic induction. The torque experienced by the orbiting electron is ehBnπm. Find n □View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.
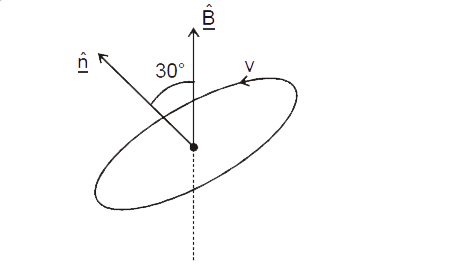
The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.View Solution
Knowledge Check
- Question 1 - Select One
An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in the circular orbit of radius R. The atom is placed in a uniform magnetic induction B such that the plane normal of electron orbit makes an angle 30∘ with B, as shown in figure. The torque experienced by electron will be
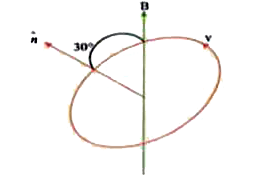 . AehB8πmBeh8πBmCeB8πmhDhB8πem
. AehB8πmBeh8πBmCeB8πmhDhB8πem - Question 2 - Select One
Magnetic dipole moment of revolving electron is
AeL2mBe2mCe2MLDemL
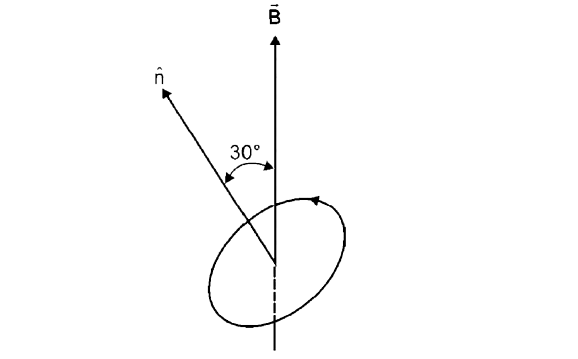
An electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.
 View Solution
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.

Obtain an expression for the orbital magnetic dipole moment of the electron.View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clock wise direction in a circular orbit. The atom is placed in a magnetic filed such that the normal to the electron orbit makes an angle of 30° with the magnetic field. Find the torque experienced by the orbiting electron.
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.

The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.View SolutionShow that the orbital magnetic dipole moment of a revolving electron isevr/2.
View Solution

