An electron is constrained to move along the central axis of a ring ofradius R having uniformly distributed charge q. Show that the electrostatic force exerted on the electron can cause itto oscillate through the centre of the ring with an angular frequency of ω=√(eq/4πε0mR3), where m is the mass of the electron ⎡⎣√qe4π∈0mR3⎤⎦
Step by step video & image solution for An electron is constrained to move along the central axis of a ring ofradius R having uniformly distributed charge q. Show that the electrostatic force exerted on the electron can cause itto oscillate through the centre of the ring with an angular frequency of omega = sqrt((eq//4pi epsilon_(0)mR^(3))), where m is the mass of the electron [sqrt((qe)/(4pi in_(0)mR^(3)))] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Partice Exercise 1.2
1 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Partice Exercise 1.3
1 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Partice Exercise 1.1
1 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs
33 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems
107 Videos
Similar Questions
A an electron is placed at the centre of the copper ring of problem 37. Show that if the electron is displaced a little, it will perform simple harmonic motion with a frequency f=12Π√eq4πε0ma3
View SolutionA particle of mass m and charge −Q is constrained to move along the axis of a ring of radius a. The ring carries a uniform charge density +λ along its length. Initially, the particle is in the centre of the ring where the force on it is zero. Show that the period of oscillation of the particle when it is displaced slightly from its equilibrium position is given by
T=2πsq√2ε0ma2λQ
View Solution
Knowledge Check
A charge +Q is uniformly distributed over a thin ring of the radius R. The velocity of an electron at the moment when it passes through the centre O of the ring, if the electron was initially at far away on the axis of the ring is (m=mass of electron, K=14πε0)
A√(2KQemR)B√(Kqem)C√(KmeQR)D√(KqemR)A dence collection of equal number of electrona and positive ions is called netural plasma. Certain solids contianing fixed positive ions surroundedby free electrons can be treated as neytral plasma. Let 'N' be the numbrer density of free electrons, each of mass 'm'. When the elctrons are subjected to an eletric field, they are displaced relatively away from the heavy positive ions. if the electric field becomes zero, the electrons begin to oscillate about the positive ions with a natural angular frequency 'ωP' which is called the plasma frequency. to sustain the oscillations, a time varying electric field needs to be applied that has an angular frequrncy ω, where a part of the energy is absorbed and a part of it is reflected. As ω approaches ωp all the free electrons are set to resonance together and all the energy is reflected. this is the explaination of high reflectivity of metals.
(2) Estimate the wavelength at which plasma reflection will occur for a metal having the density of electrons N≈4×1027m−3. Taking ε0=1011 and mass m≈10−30, where these quantities are in proper SI units.A(a) 800nmB(b) 600nmC( c ) 300nmD(d) 200nmWhich statement is true :-
(i) A ring of radius R carries a uniformly distributed charge +Q. A point charge -q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a smiple harmonic motion along the axis of the ring.
(ii) Electrons move from a region of higher potential to that of lower potentialAonly (i)Bonly (ii)C(i), (ii)Dnone of them
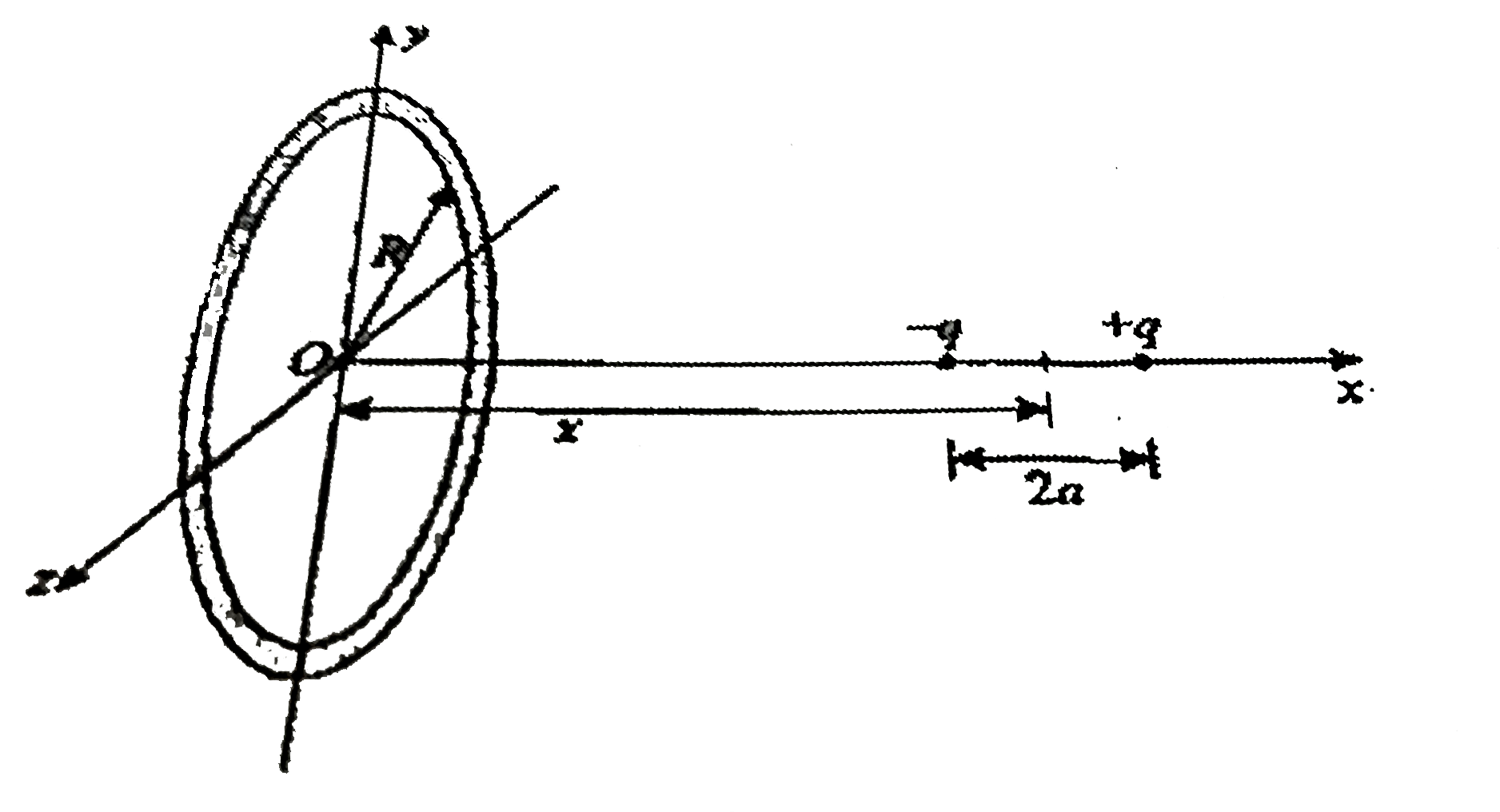
An electric dipole is placed at a distance x from centre O on the axis of a charged ring of radius R and charge Q uniformly distributed over it.
(a) Find the net force acting on the dipole
(b) What is the work done in rotating the dipole through 180∘?
[(a)aqQ2πε0(R2−2x2(R2+x2)3/2),(b)aqQxπε0(R2+x2)3/2]
View SolutionThe electric intensity Eat a point on the axis ofa ring of radius a at a distance x from its centre is given by
14πε0qx(a2+x2)3/2
where q is charge on ring.
An electron is constrained to move along the axis of this ring. Show that the electron can perform oscillations whose frequency is given by
ω=(eq4πε0ma3)1/3
Where e is the charge on electron:
View SolutionA ring of radius R is having two charges q and 2q distributed on its two half parts. The electric potentiasl at a point on its axis at a distance of 2√2R from its centre is (k=14πε0)
View SolutionA charge q=10μC is distributed uniformly over the circumference of a ring of radius 3m placed on x-y placed with its centre art origin. Find the electric potential at a point P(0,0,4m)
View SolutionA thin ring of 10 cm radius carries a uniformly distributed charge. The ring rotates at a constant angular speed of 40πrad s−1 about its axis, perpendicular to its plane. If the magnetic field at its centre is 3.8×10−9T, then the charge carried by the ring is close to (μ0=4π×10−7N/A2)
View Solution
