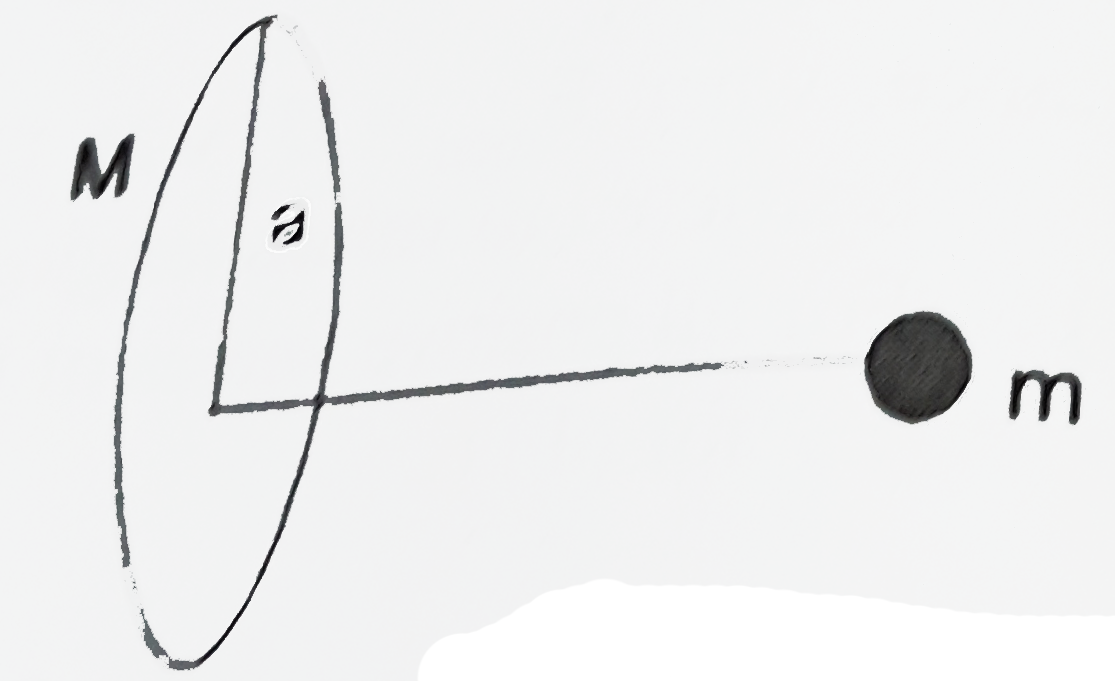
A particle of mass m and charge −Q is constrained to move along the axis of a ring of radius a. The ring carries a uniform charge density +λ along its length. Initially, the particle is in the centre of the ring where the force on it is zero. Show that the period of oscillation of the particle when it is displaced slightly from its equilibrium position is given by
T=2πsq√2ε0ma2λQ
The correct Answer is:A
To solve the problem, we need to analyze the motion of a charged particle along the axis of a charged ring and derive the expression for the period of oscillation when it is displaced slightly from its equilibrium position.
1. Understanding the System:
- We have a ring of radius a with a uniform charge density +λ.
- A particle of mass m and charge −Q is positioned at the center of the ring, where the net force acting on it is zero.
2. Total Charge on the Ring:
- The total charge Qring on the ring can be calculated using the circumference of the ring:
Qring=λ⋅(2πa)
3. Electric Field at a Distance x:
- When the particle is displaced by a small distance x along the axis of the ring, we need to find the electric field E at that point.
- The electric field at a distance x from the center of the ring along its axis is given by:
E=14πϵ0⋅Qring⋅x(a2+x2)3/2
- Substituting for Qring:
E=14πϵ0⋅(2πaλ)⋅x(a2+x2)3/2=λx2ϵ0(a2+x2)3/2
4. Force on the Particle:
- The force F acting on the particle due to the electric field is given by:
F=−Q⋅E=−(−Q)⋅λx2ϵ0(a2+x2)3/2=λQx2ϵ0(a2+x2)3/2
5. Approximation for Small Displacements:
- For small displacements, where x is much smaller than a (i.e., x≪a), we can approximate a2+x2≈a2.
- Thus, the force simplifies to:
F≈λQx2ϵ0a3
6. Comparing with Hooke's Law:
- The force can be expressed as F=−kx where k is the effective spring constant. Therefore, we have:
k=λQ2ϵ0a3
7. Finding the Period of Oscillation:
- The period T of oscillation for a mass-spring system is given by:
T=2π√mk
- Substituting for k:
T=2π√m⋅2ϵ0a3λQ
8. Final Expression:
- Rearranging gives us the final expression for the period of oscillation:
T=2π√2ϵ0ma2λQ
- We have a ring of radius a with a uniform charge density +λ.
- A particle of mass m and charge −Q is positioned at the center of the ring, where the net force acting on it is zero.
- The total charge Qring on the ring can be calculated using the circumference of the ring:
Qring=λ⋅(2πa)
- When the particle is displaced by a small distance x along the axis of the ring, we need to find the electric field E at that point.
- The electric field at a distance x from the center of the ring along its axis is given by:
E=14πϵ0⋅Qring⋅x(a2+x2)3/2
- Substituting for Qring:
E=14πϵ0⋅(2πaλ)⋅x(a2+x2)3/2=λx2ϵ0(a2+x2)3/2
- The force F acting on the particle due to the electric field is given by:
F=−Q⋅E=−(−Q)⋅λx2ϵ0(a2+x2)3/2=λQx2ϵ0(a2+x2)3/2
- For small displacements, where x is much smaller than a (i.e., x≪a), we can approximate a2+x2≈a2.
- Thus, the force simplifies to:
F≈λQx2ϵ0a3
- The force can be expressed as F=−kx where k is the effective spring constant. Therefore, we have:
k=λQ2ϵ0a3
- The period T of oscillation for a mass-spring system is given by:
T=2π√mk
- Substituting for k:
T=2π√m⋅2ϵ0a3λQ
- Rearranging gives us the final expression for the period of oscillation:
T=2π√2ϵ0ma2λQ
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
A quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
View Solution
Knowledge Check
A ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32Charge q is uniformly spreade on a thin ring of radius R. The ring rotates about its axis with a uniform frequency f Hz. The magnitude of magnetic induction at the centre of the ring is
Aμ0qf2πRBμ0qf2RCμ0q2fRDμ0q2πfRA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
if x<<a, the particle of mass m will:Aperform oscillatory motionBperform S.H.M.CbothDNone
Potential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View SolutionA smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?

View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
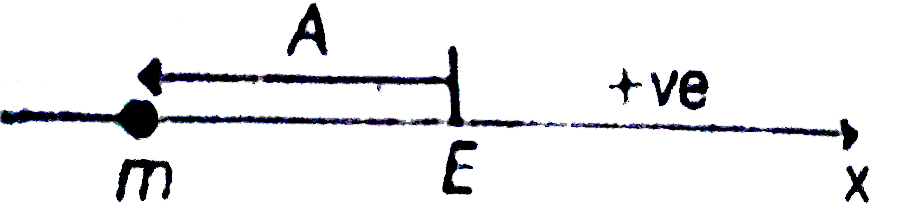
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
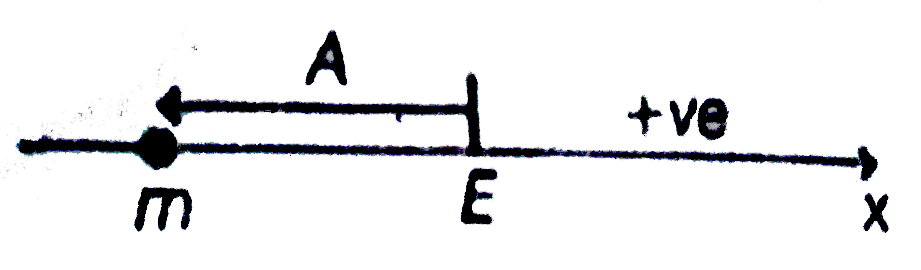
View Solution
