An element with emfε and interval resistance r is connected across an external resistance R. The maximum power in external circuit is 9W. The current flowing through the circuit in these conditions is 3A. Then which of the following is // are correct ?
ε=6V
r=R
r=1Ω
r=3Ω
The correct Answer is:A, B, C
To solve the problem step by step, we will analyze the given information and apply the relevant formulas.
Step 1: Understand the Circuit
We have an EMF source (ε), an internal resistance (r), and an external resistance (R) connected in series. The current flowing through the circuit is given as 3 A, and the maximum power in the external circuit is given as 9 W.
Step 2: Use the Power Formula
The power (P) dissipated across the external resistance R can be expressed as:
P=I2R
Where:
- I is the current flowing through the circuit.
Given that the maximum power Pmax=9W and I=3A, we can rearrange the formula to find R:
9=(3)2R
9=9R
R=1Ω
Step 3: Use the Maximum Power Transfer Theorem
For maximum power transfer, the external resistance (R) should be equal to the internal resistance (r):
R=r
Thus, we have:
r=1Ω
Step 4: Find the EMF (ε)
Using Ohm's law, we can find the EMF (ε) of the source. The total resistance in the circuit is:
R+r=1+1=2Ω
Using Ohm's law:
I=ER+r
Substituting the known values:
3=E2
Thus:
E=3×2=6V
Step 5: Summary of Results
From the calculations, we find:
- EMF (ε) = 6 V
- Internal Resistance (r) = 1 Ω
- External Resistance (R) = 1 Ω
Conclusion
The correct answers based on the calculations are:
- EMF (ε) = 6 V
- Internal Resistance (r) = 1 Ω
- External Resistance (R) = 1 Ω
We have an EMF source (ε), an internal resistance (r), and an external resistance (R) connected in series. The current flowing through the circuit is given as 3 A, and the maximum power in the external circuit is given as 9 W.
The power (P) dissipated across the external resistance R can be expressed as:
P=I2R
Where:
- I is the current flowing through the circuit.
9=(3)2R
9=9R
R=1Ω
For maximum power transfer, the external resistance (R) should be equal to the internal resistance (r):
R=r
Thus, we have:
r=1Ω
Using Ohm's law, we can find the EMF (ε) of the source. The total resistance in the circuit is:
R+r=1+1=2Ω
Using Ohm's law:
I=ER+r
Substituting the known values:
3=E2
Thus:
E=3×2=6V
From the calculations, we find:
- EMF (ε) = 6 V
- Internal Resistance (r) = 1 Ω
- External Resistance (R) = 1 Ω
The correct answers based on the calculations are:
- EMF (ε) = 6 V
- Internal Resistance (r) = 1 Ω
- External Resistance (R) = 1 Ω
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Assertion - Reasoning
6 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Comprehension
13 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Single Correct
60 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
A cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionA cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation o P.D. Across R, verses 'R.
View Solution
Knowledge Check
In a circuit a cell with internal resistance r is connected to an external resistance R. The condition for the maximum current that drawn from the cell is
AR=rBR<rCR>rDR=0
In the circuit, the current flowing through 10Ω resistance is
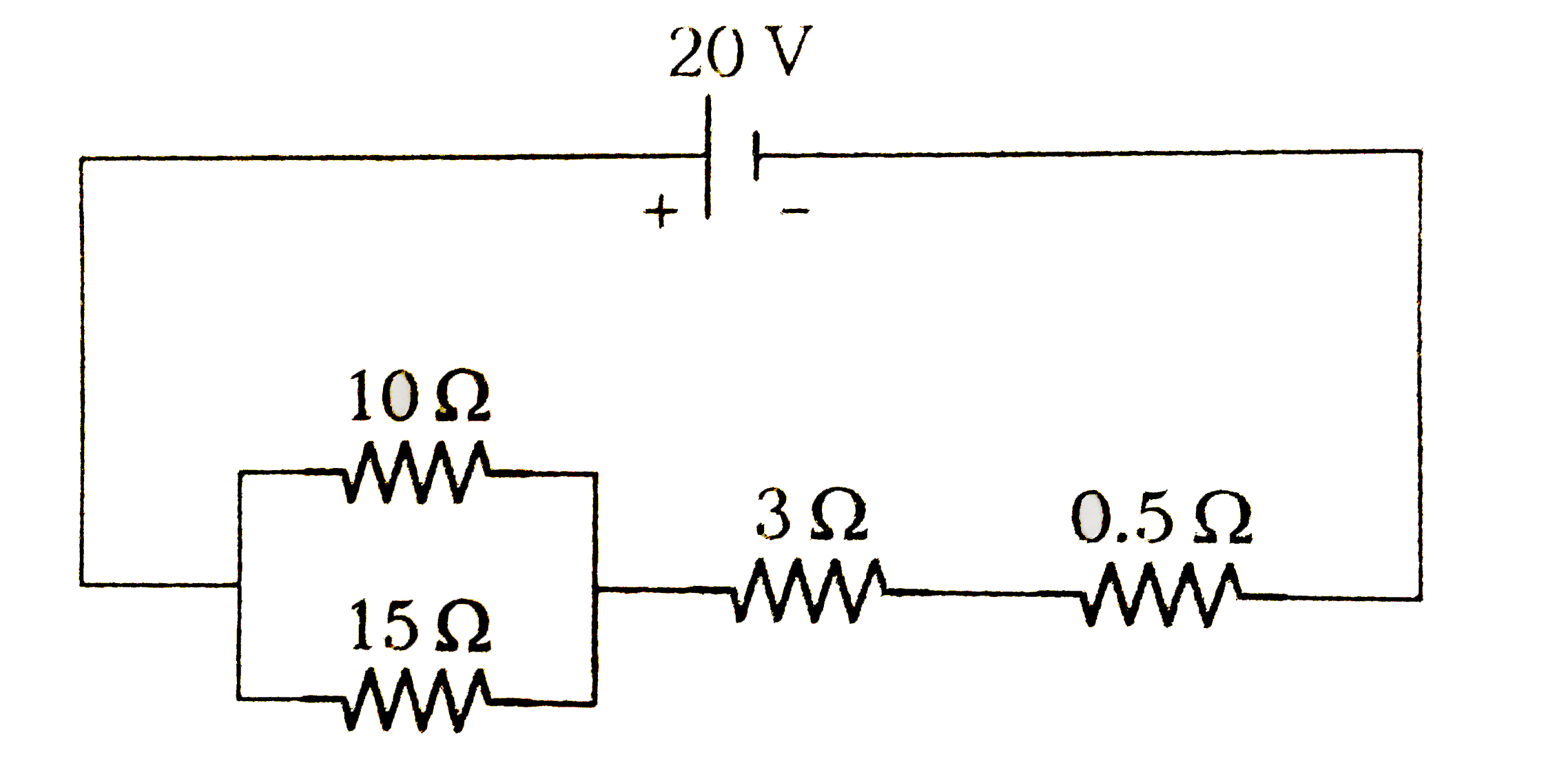
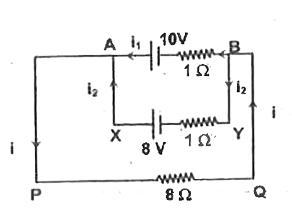
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
View SolutionIn the given circuit current flowing through 2 Omega resistance is
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View Solution2A cell having an emf ε and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionThe emf of a battery is 2V and its internal resistance is 0.5Ω the maximum power which it can deliver to any external circuit will be
View Solution
