Question

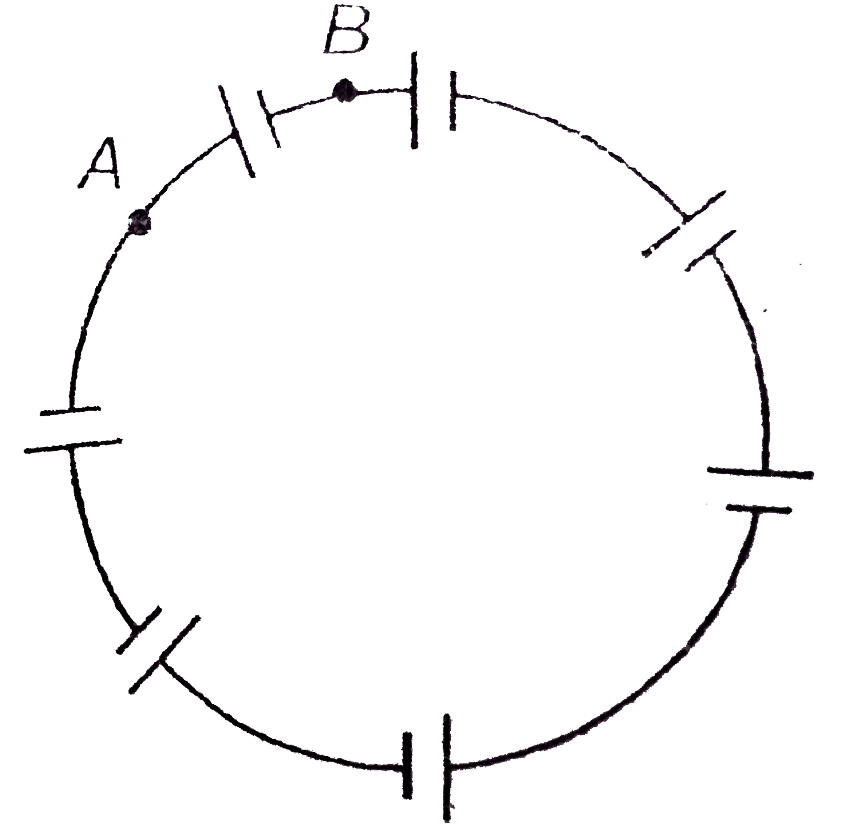
n identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is

Options

A. `(nE)/(R + nr)`
B. `(nE)/(nR + r)`
C. `E/(R + nr)`
D. `(nE)/(R + r)`

Answer

A

Explanation

To solve the problem, we need to determine the current flowing through the external resistance $$R$$ when $$n$$ identical cells, each with an electromotive force (e.m.f.) $$E$$ and internal resistance $$r$$, are connected in series with the external resistance $$R$$.

1. Identify the Total e.m.f. in the Circuit:
When \( n \) identical cells are connected in series, the total e.m.f. \( E_{\text{total}} \) of the combination is given by:
\( E_{\text{total}} = nE \)

2. Identify the Total Internal Resistance:
The internal resistance of each cell is \( r \). Since they are connected in series, the total internal resistance \( r_{\text{total}} \) of the combination is:
\( r_{\text{total}} = nr \)

3. Set Up the Circuit Equation:
According to Kirchhoff's voltage law, the sum of the potential differences (voltage) in a closed circuit must equal zero. For our circuit, we have:
\( E_{\text{total}} = I(R + r_{\text{total}}) \)
Substituting the values we found:
\( nE = I(R + nr) \)

4. Solve for the Current \( I \):
Rearranging the equation to solve for the current \( I \):
\( I = \frac{nE}{R + nr} \)

5. Final Expression for Current:
Thus, the current through the external resistance \( R \) is:
\( I = \frac{nE}{R + nr} \)